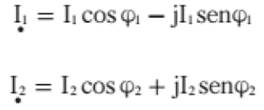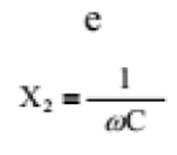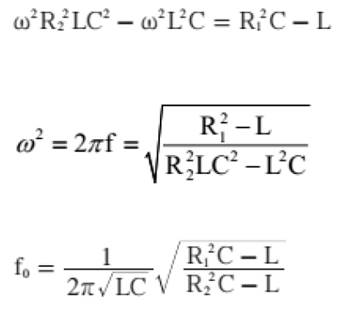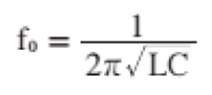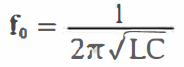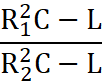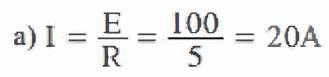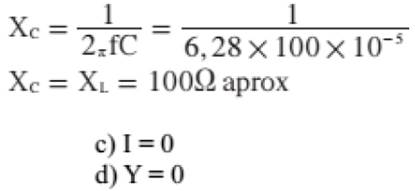|
RESSONÂNCIA EM CIRCUITOS EM PARALELO Vimos
que um circuito em série está em ressonância quando as componentes verticais
(EL e Ec) da tensão aplicada ao circuito são iguais. Dizemos
que um circuito em paralelo entra em ressonância, QUANDO A SOMA DAS
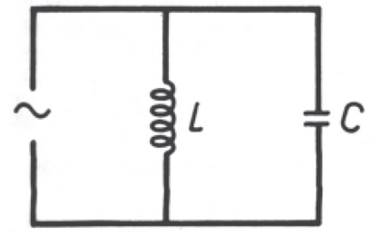
COMPONENTES VERTICAIS DAS CORRENTES NOS DlVERSOS RAMOS É IGUALA ZERO. Consideremos
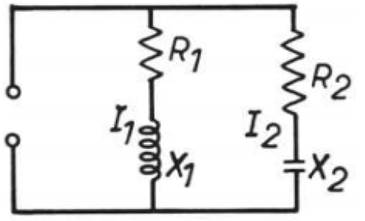
o circuito
No
ramo 1 a corrente está atrasada ф1 graus em relação
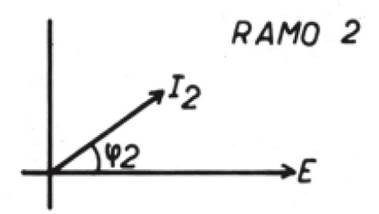
tensão, e no ramo 2 está adiantada ф2 graus em relação
à tensão:
Os vetores I1
e I2 podem ser considerados iguais à soma de duas componentes: uma
componente horizontal (componente ATIVA, responsável pela transformação da
energia elétrica em calor) e outra vertical (REATIVA), e podem ser expressas
da seguinte maneira:
A
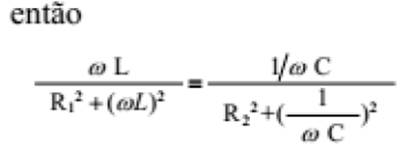
condição de ressonância é
Eliminando os denominadores e dividindo todos os termos por ω
temos a
Equação Geral para o Cálculo da Frequência de Ressonância no Circuito em
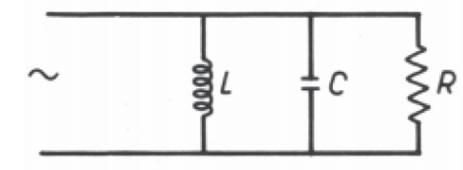
Paralelo. Se o circuito tivesse o aspecto abaixo (ramos indutivo e capacitivo com resistência
desprezível),
a equação para o
cálculo da fregüêncra de ressonância ficaria resumida a
porque os termos R1
e R2, que se referem aos braços indutivo e capacitivo, seriam
nulos. A corrente total em ressonância seria apenas a corrente solicitada
pelo Se tivéssemos o
circuito abaixo, com indutância pura num dos braços e capacitância pura no
outro,
a frequência
de ressonância seria calculada também com a equação simplificada
pelo
mesmo motivo acima. A corrente total neste circuito, quando em ressonância,
seria nula, embora houvesse corrente nos dois ramos. O circuito estaria
oferecendo, portanto, uma impedância infinita. Tal circuito não tem
existência real, mas é possível reduzir as resistências dos braços do
circuito a valores muito pequenos (praticamente desprezíveis), obtendo-se
resultados bem próximos do que foi dito, com vasta aplicação no campo da
Eletrônica. Duas
condições ainda poderiam ser observadas num circuito em paralelo: -Se R1²C>L
e R2²C<L, ou R1²C<L e R2²C>L, a
quantidade
Seria negativa e sua raiz quadrada seria imaginária:
sob estas condições, o circuito nunca poderia entrar em ressonância;
isto é, O CIRCUITO ENTRARIA EM RESSONANCIA
EM QUALQUER FREQUÊNClA Podemos resumir nossas observações dizendo que um circuito em paralelo oferece o máximo de impedância quando está em
ressonância, solicitando então o mínimo de corrente da fonte, ao contrário do
circuito em série, que oferece o mínimo de impedância ao entrar em
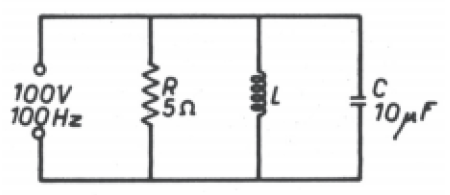
ressonância. EXEMPLO:
a) Se O circuito estivesse em ressonância, qual a corrente
solicitada da fonte? b) Qual o valor de "XL" para que o
circuito entre em ressonância? c) Se não existisse qual seria a corrente total, quando o
circuito estivesse em ressonância? d) Qual seria a admitância do circuito, se ele estivesse em
ressonância? (Nas condições do item c.) SOLUÇÃO:
b) "XL" deverá ser igual a “XC”para
que o circuito entre em ressonância:
Correção do
Fator de Potência O fator de potência de
um circuito deve ser mantido aproximadamente igual a 1. Isto, porque um fator
de potência muito baixo implica no encarecimento da instalação e em maiores perdas
no cobre, pois são necessárias maior corrente e maior potência aparente para
a obtenção de uma determinada potência real, o que se pode concluir
observando a expressão abaixo:
A tensão aplicada aos
circuitos nas residências fábricas, etc., é constante e, portanto, a corrente
fornecida aos mesmos pode ser demasiado elevada, se o fator de potência for
muito baixo. O grande número de
aparelhos indutivos (motores, equipamento auxiliar para lâmpadas
fluorescentes, máquinas de soldar, etc.) normalmente utilizados nas
instalações residenciais, comerciais e industriais, resulta em um fator de
potencia baixo e em atraso. Para corrigir o fator
de potência, reduzindo suas consequências e ao mesmo tempo cumprindo
exigências constantes da legislação em vigor, no que se refere às instalações
elétricas, são ligados capacitares em paralelo com o elemento (ou elementos)
causador(es) da dificuldade. Certos motores de C.A.,
chamados motores síncronos, são também utilizados para o mesmo fim. |