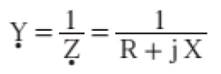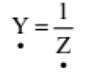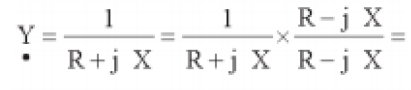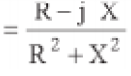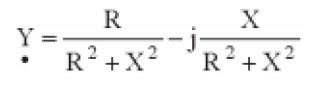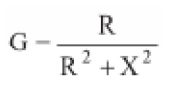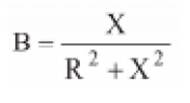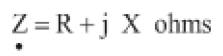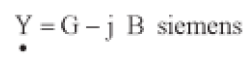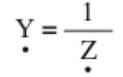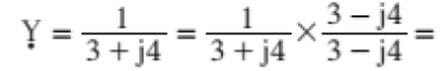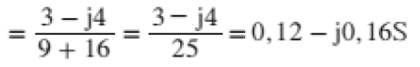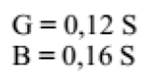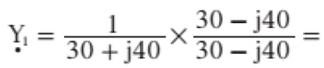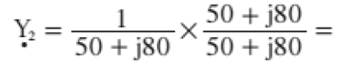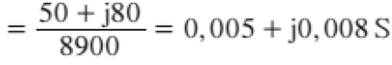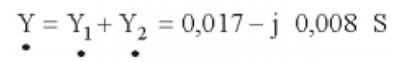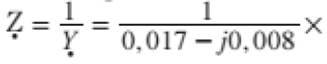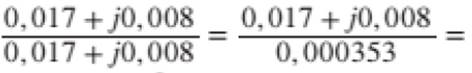|
ADMITÂNCIA(Y), CONDUTÂNCIA(G)
E SUSCEPTÂNCIA(B) Foi dado o nome de admitância ao inverso da impedância:
A admitância exprime, portanto. a facilidade que o circuito
ou elemento do circuito oferece ao estabelecimento de uma corrente elétrica.
E medida em SIEMENS Como sabemos, SIEMENS é o mesmo que AMPÈRE/VOLT, logo a
admitânc ia de um circuito corresponde à corrente que pode ser produzida no
mesmo para cada volt aplicado aos seus
Assim como a Impedancia é a soma da resistência com a reatâncla, Z=R+jX
a admitância tambem é a
soma dos inversos da resistência e da reatância. é
denominado SUSCEPTÂNCIA. A condutância e a susceptância são,
evidentemente, medidas em SIEMENS e a determinação dos seus valores não é um simples
cálculo aritmético.
A componente real (componente no eixo horizontal) do vetor Y é o inverso
da componente real do vetor Z, e portanto é a condutância:
A componente imaginária (componente no eixo vertical) do vetor Y é o
inverso da componente imaginária do veter Z, e portanto é a susceptância:
Resumindo, representamos a seguir a impedância e a admitância na forma
binômia:
Na resolução dos circuitos em paralelo, é conveniente trabalhar com a
admitância. Ao fazermos representaçöes gráficas é convemente tomar a tensão
como referência, visto que esta grandeza apresenta o mesmo valor entre os
terminais de todos os ramos do circuito. Na resolução dos circuitos mistos
devem ser aplicados, onde couberem, os conhecimentos referentes aos circuitos
em série e em paralelo. EXEMPLOS: 1-Uma impedância de 3 + j 4 ohms foi ligada a uma fonte de 100 V.
Determinar: a) a condutância do circuito; b) a susceptância do circuito; c) a admitância do circuito. SOLUÇÃO:
2-Um circuito de CA. em paralelo é ligado a uma fonte de
220V 60 Hz. Sabendo que um dos ramos do circuito contém 30Ω de
resistência e 40Ω de reatância indutiva, e que o outro ramo apresenta
50Ω de resistência e 80Ω de reatância capacitiva, determinar. a) a impedância do circuito; b) a corrente solicitada da fonte; c) o fatur de potência do circuito; d) a impedância de cada ramo do circuito; e) o fator de potência de cada ramo do circuito; f) a admitância do circuito; g) a susceptância do circuito; h) a condutância do circuito; i) a potência real do circuito; j) a potência aparente do circuito. SOLUÇÃO: — Impedância do ramo com reatância indutiva:
-Fator de potência do ramo com reatäncia indutiva: cos 53°
10’ = 0,6 aprox. (atrasado) -Impedância do ramo com reatåncia capacitiva:
- Fator de potência do ramo com reatåncia capacitiva: cos
-58° = aprox. 0,5 (adiantado) - Admitância
do ramo indutivo:
-Admitância do ramo capacitivo:
-Admitância
total:
- Condutância do
circuito: G=0,017 s -Susceptância do circuito: B=0,008 S - Impedância do circuito:
-Fator
de potência do circuito:
-Potência
real do circuito:
-Potência aparente do circuito:
|