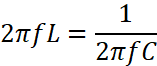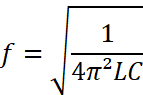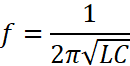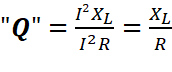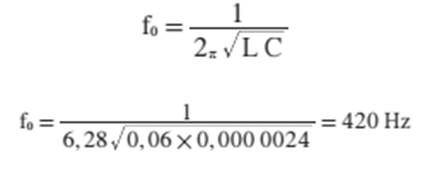|
RESSONÂNCIA
EM CIRCUITOS EM SÉRIE Quando é estabelecida a igualdade entre a
reatância indutiva e a reatância capacitiva, o que determina igualdade entre
as tensões Ec e EL, dizemos que o circuito
está em RESSONÂNCIA. Esta condição é desejável em vários
circuitos usados em Eletrônica, mas pode trazer consequências desagradáveis,
com danos para os elementos de um circuito, quando não é prevista. Sabemos
que a reatância indutiva é diretamente proporcional à frequência e que a
reatância capacitiva depende inversamente da mesma. Assim, quando alimentamos
um circuito com uma fonte de C.A. e fazemos a frequência variar desde um
valor praticamente nulo a um valor alto, podemos observar o crescimento da
reatância indutiva e a queda da reatância capacitiva. Numa determinada
frequência, as duas grandezas tornam-se iguais e o circuito apresenta
características especiais que correspondem à condição denominada ressonância.
Estas características, são as seguintes: a) a impedância do circuito toma-se mínima,
ficando reduzida ao valor da resistência; b) a intensidade da corrente é máxima, como
consequência do exposto no item anterior, e limitada apenas pelo valor da
resistência; c) o circuito toma-se resistivo; d) todas as energias aplicadas ao circuito
são gasta para vencer sua resistência: E = ER P = S = EI cos ф=
1 Q = 0 A frequência em que um circuito em série
entra em ressonância pode ser determinada com a expressão
f0 =frequência de ressonância,
em HERTZ (Hz) L = autoindutância do circuito, em HENRYS
(H) C= capacitância do circuito, em FARADS (F) Com efeito, se XL
= XC
Um exame da equação em apreço faz-nos
concluir que a resistência do circuito não influi na sua frequência de
ressonância e que esta só depende do PRODUTO LC.
Isto significa que circuitos com valores diferentes para L e para C podem
entrar em ressonância na mesma frequência, desde que os produtos LC
sejam iguais. Convém esclarecer, porém, que a resistência
do circuito influi no que é conhecido como FATOR Q do circuito
ressonante, isto é, a relação entre a potência reativa referente à indutância
(ou à capacitância) e a potência real do circuito: FATOR Normalmente
a resistência do circuito é constituída principalmente pela resistência de
uma bobina, de modo que é comum fazer referência à resistência da bobina e à
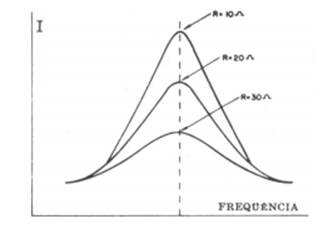
sua reatância indutiva. A variação de corrente num circuito quando
a frequência da fonte é variada pode ser representada graficamente
constituindo o que uma CURVA DE RESSONÂNCIA.
Fig.
19 Se traçarmos curvas de ressonância de um circuito
série R-L-C mantendo constante o valor de “R”, observaremos que as formas das
curvas variarão se forem variados os valores de “L” e “C”; O CRESCIMENTO DA
INDUTÂNCIA E A REDUÇÃO DA CAPACITÂNCIA AGUÇAM A CURVA. A variação da resistência, com “L” e “C”
constantes, afeta a ordenada máxima e aguça a curva de ressonância. EXEMPLO: Num circuito de CA em série temos 0,06H de
indutância, 2,4 µF de capacitância e 350Ω de resistência não indutiva.
Qual a frequência de ressonância do Circuito?
|