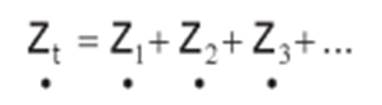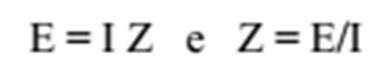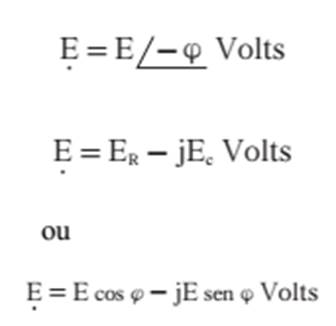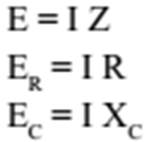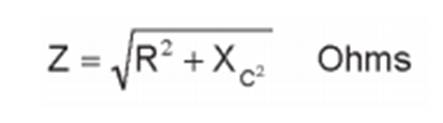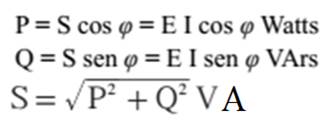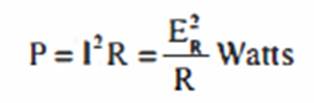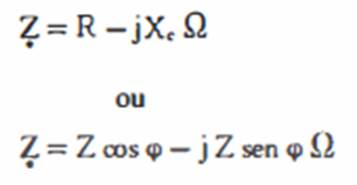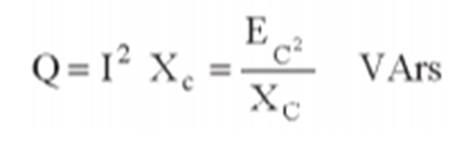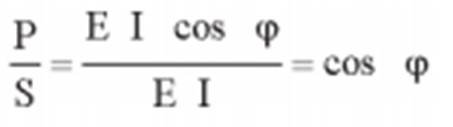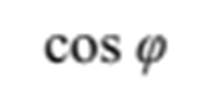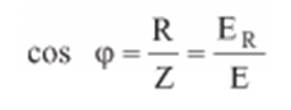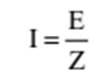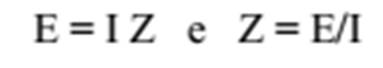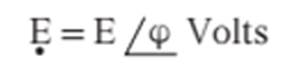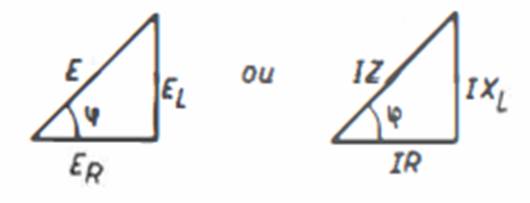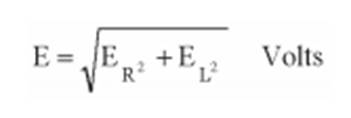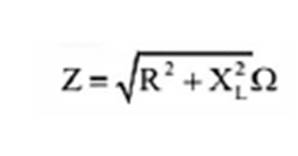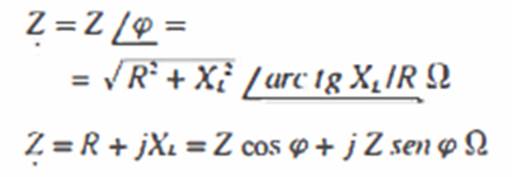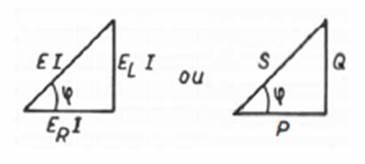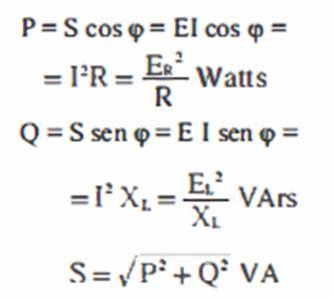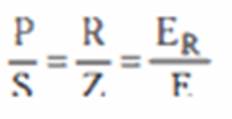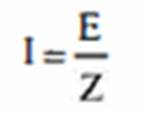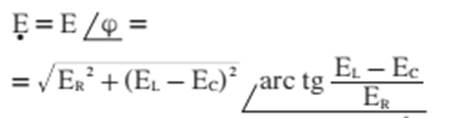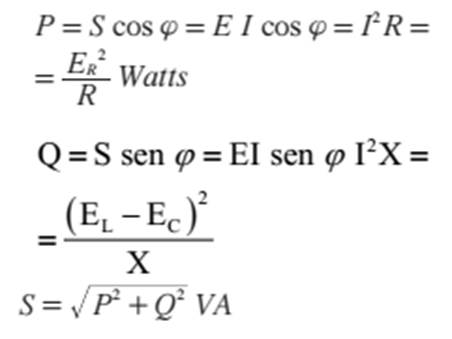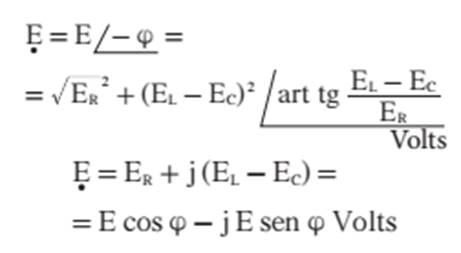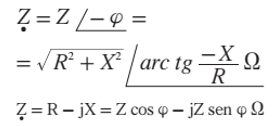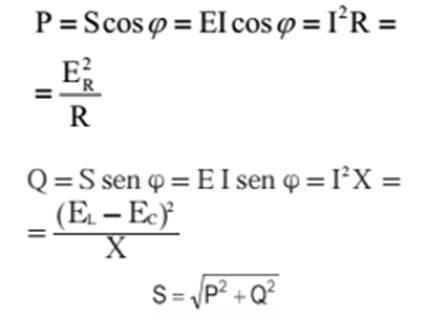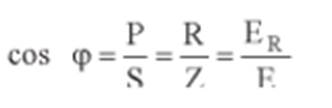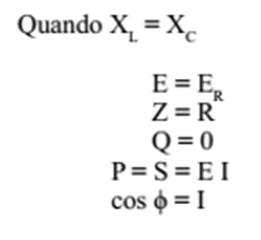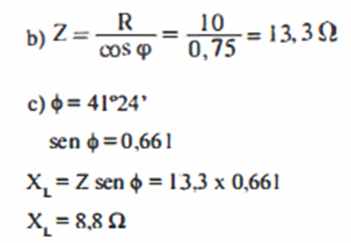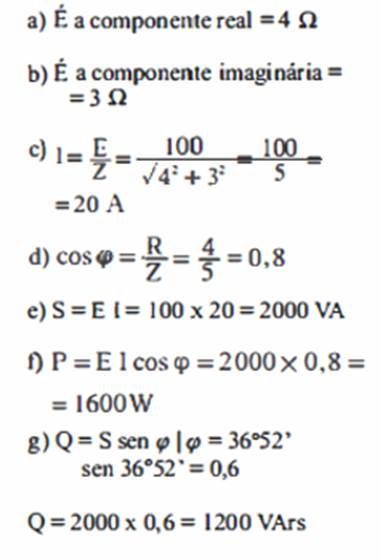|
CIRCUITOS MONOFÁSICOS DE C.A. (CIRCUITOS EM SÉRIE, TIPOS R-C, R-L
E R-L.C) Os
circuitos de corrente alternada em sene apresentam as mesmas características
gerais dos circuitos de corrente contínua: -a
intensidade da corrente é a mesma em qualquer parte do circuito; -a
tensão aplicada ao circuito é igual à
soma das tensões parciais nos diversos elementos dele. Entretanto, em
corrente alternada a soma em apreço é vetorial, como será discutido a seguir;
-a impedância total ou equivalente é a soma das
impedâncias parciais. Na determinação da impedância total, associamos
primeiro as resistências, indutâncias e capacitâncias, e, então.
representamos a Impedância na forma polar ou binômia. Às vezes, não são conhecidos
os valores das resistências, indutâncias e capacitâncias parciais, mas são
oferecidos os valores das impedâncias dos diversos elementos do circuito, O
que facilita ainda mais o cálculo da impedância total, resumindo-se numa soma
das quantidades conhecidas:
No decorrer deste
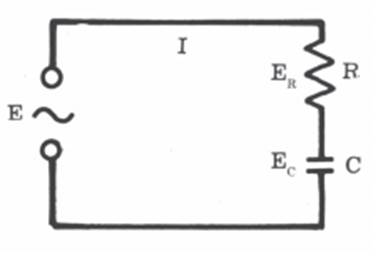
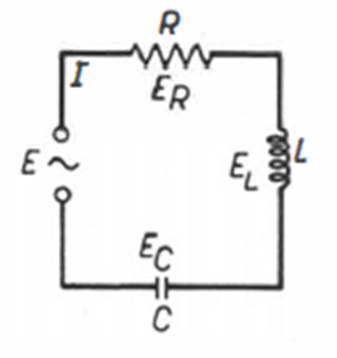
estudo serão apresentados exemplos que tornarão mais claro o que foi exposto. CIRCUITO EM SÉRIE TIPO R-C
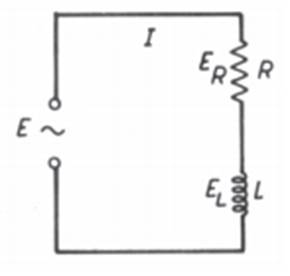
R
e C simbolizam, respectivamente, a resistência equivalente e a
capacitância equivalente do circuito. A
dificuldade encontrada pela fonte para estabelecer uma corrente no circuito é
determinada pela soma vetorial de R e X: Z = soma vetorial de R
e Xc A
intensidade da corrente elétrica obedece à Lei de Ohm:
donde
Neste
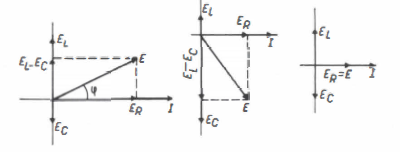
circuito, a tensão E a soma vetorial das componentes ER e EC
Podemos representar vetorialmente as tensões no circuito, tomando como
referência a corrente. É comum, aliás, considerar o vetor corrente no eixo de
referência nos circuitos em série, tendo em vista que a intensidade da
corrente é a mesma em qualquer parte do circuito.
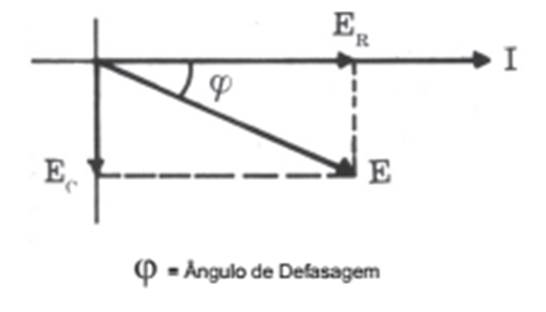
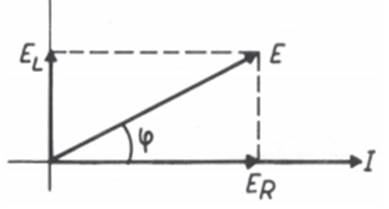
FIG. 02 Observa-se que o ângulo
de defasagem entre a tensão aplicada ao circuito e a corrente no circuito é
menor do que 90º, e seu valor depende da razão entre os valores de R e de Xc. O vetor E (tensão
aplicada ao circuito) pode ser representado nas formas polar e binômia:
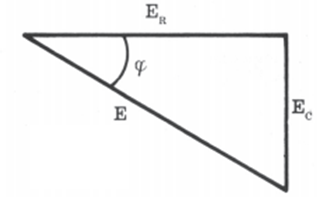
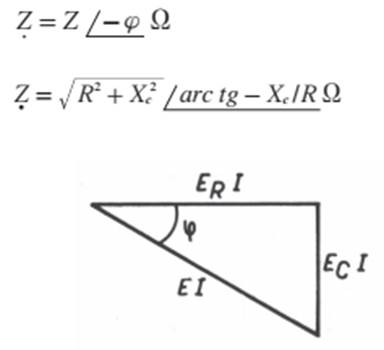
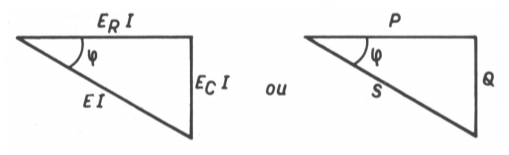
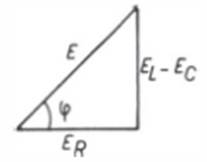
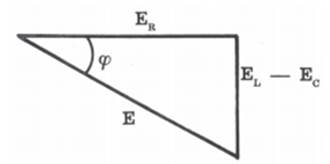
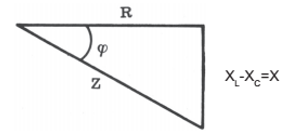
O vetor E e suas componentes formam um triângulo retângulo TRIÂNGULO DAS TENSÕES
FIG.
03 permitindo-nos escrever
a expressão abaixo, que nos dá o módulo da tensão E:
E inoperante o uso do sinal
(-) na determinação do módulo do vetar, contudo, seu uso é indispensável na
determinação da posição do vetor em relação ao eixo de referência. Sabemos que
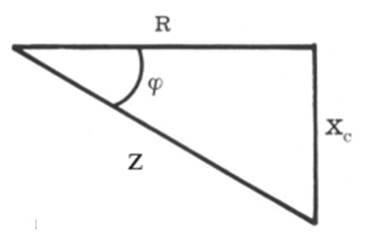
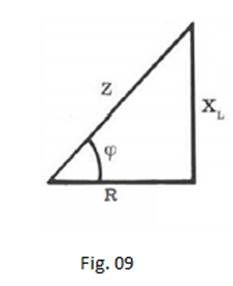
e se dividimos todos os
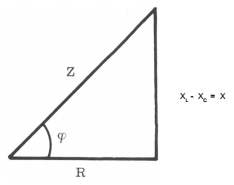
termos por I temos o triângulo-retângulo abaixo: TRIÃNGULO DAS IMPEDÂNCIAS
FIG.
04 A partir deste
triângulo podemos achar o valor da impedância:
A impedância não é uma
grandeza vetorial, mas é normal a sua representação como um vetor, dada a conveniência
desta medida. Assim, podemos dar a impedância nas formas polar e binômia:
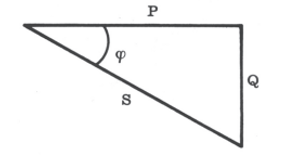
FIG.
05 P=
ER I = potência real Q=
EC I = potência reativa S = E I = potência
aparente Do triângulo em apreço
podemos concluir que
E fazendo substituições
de termos de acordo com a Lei de Ohm:
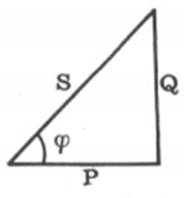
Multiplicando os lados
do triângulo das tensões por I, obtemos o TRIANGULO DAS POTÊNCIAS:
Neste circuito, o fator
de potência sempre maior que zero e menor que 1, pois sempre há gasto de
energia para vencer resistência, sem que toda a energia aplicada ao circuito
tenha essa finalidade: Fator
de Potência.
Observa-se que o fator
de potência do circuito corresponde ao cosseno do ângulo de defasagem entre a
tensão aplicada ao circuito e a corrente no circuito. É NORMAL USAR A
EXPRESSÃO
PARA
DESIGNAR O FATOR DE POTÊNCIA
Como a corrente está
adiantada em relação à tensão, é usual dizer que o circuito apresenta FATORDE
POTÊNCIA ADIANTADO. No estudo dos outros
circuitos evitaremos repetir todas as razões que levaram a determinadas
conclusões e, assim, aconselhamos um estudo atento do circuito R-C, para
melhor compreensão dos parágrafos seguintes. CIRCUITO EM
SÉRIE TIPO R-L
R L simbolizam, respectivamente.
a resistência equivalente e a autoindutância equivalente do circuito. A
impedância do circuito é a soma vetorial de R e XL. A
intensidade da corrente é
donde
A tensão aplicada ao
circuito (E) é a soma vetorial das componentes ER e EL:
FIG.
07 O valor de ф
depende da razão entre os valores de R e XL Representando o vetor E
nas formas polar e binômia:
E=ES
+ jEL=Ecosф
+ jEsenф Volts O triângulo das tensões
tem o seguinte aspecto:
FIG.
08 o que permite a determinação
do módulo da tensão E, de acordo com o teorema de Pitágoras:
ou na forma polar
Dividindo os termos
correspondentes aos lados do triângulo das tensões por I, obtemos o triângulo
das impedâncias:
Representando
vetorialmente a impedância:
Do mesmo modo que no
circuito R-C, podemos obter o triângulo das potências:
P
= ERI = potência real Q
= EL I = potência reativa S
= EI = potência aparente
O fator de potência do
circuito é sempre maior do que zero e menor do que I, e, como a corrente está
atrasada em relação à tensão, dizemos que o circuito apresenta FATOR DE
POTÊNCIA EM ATRASO: Fator
de Potência = Cos ф
CIRCUITO EM
SÉRIE TIPO R-L-C
R=resistência
equivalente do circuito L=autoindutância
equivalente do circuito C= Capacitância
equivalente do circuito Z=soma vetorial de R,
donde
E = I Z e Z = E/I Neste
tipo de circuito, três situações podem ocorrer:
EL>EC,
porque XL>XC EL<EC,
porque XL<XC EL=EC,
porque XL=XC O primeiro caso o
circuito comporta-se como um circuito indutivo (RL), no segundo caso toma-se
capacitivo e no último caso apresenta praticamente as características de um
circuito puramente resistivo. É interessante observar
que EL- EC representa a SOMA de + EL com -EC: EL+(-EC)
=EL=EC vejamos
as características do circuito em cada uma das situações que podem existir: QUANDO XL > XC TRIÂNGULO DAS TENSÕES
Fig.
13
TRIÂNGULO DAS IMPEDÂNCIAS
Fig.14
TRIÂNGULO DAS POTÊNCIAS
Fig.
15
Fator
de Potência (atrasado)
QUANDO XL<XC TRIÂNGULO
DAS TENSÕES
Fig.
16
TRIÂNGULO
DAS IMPEDÂNCIAS
Fig.
17
TRIÂNGULO
DAS POTÊNCIAS
Fig.
18
Fator
de Potência (adiantado)
EXEMPLOS 1 -Um amperimetro,
um voltímetro e um vattímetro são I igados no circuito de um motor de indução
monofásico e indica,n, respectivamente, 1 O A, 220 V e 1.900W DETERMINAR: a) o
fator de potência do motor; b) a
impedância do circuito; c) a
resistência efetiva. SOLUÇÃO:
2 - 75% da energia
aplicada por segundo a um circuito de C.A. são transformados em calor. O
circuito, que é indutivo, apresenta uma resistência de 10 Ω. DETERMINAR: a) o fator de potência
do circuito; b) A impedância do
circuito; c) A reatância indutiva
do circuito. SOLUÇÃO:
3 - Uma impedância de 4
- j3 ohms foi ligada a uma fonte de 100V. Determinar os seguintes elementos
do circuito: DETERMINAR: a) a resistência
efetiva; b) a reatância; c) a intensidade da
corrente; d) o fator de potência; e) a potência aparente; f) a potência real; g) a potência reativa. SOLUÇÃO:
|