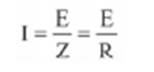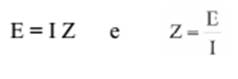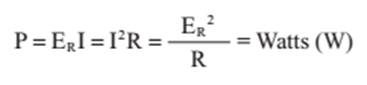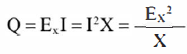CIRCUITOS MONOFÁSICOS IDEAIS

 

 

Um circuito monofásico é aquele alimentado por uma única tensão alternada.

 

O estudo dos circuitos de C.A. deve ser precedido pela análise de três circuitos ideais, isto é, pelo estudo do que ocorreria se pudéssemos ter circuitos com resistência pura, com indutância pura e com capacitância pura.

 

Compreendida a atuação de cada um desses parâmetros, torna-se mais fácil assimilar o que ocorre num circuito real, onde atuam simultaneamente.

 

De acordo com o que já foi estudado, qualquer circuito de corrente alternada apresenta resistência- reatância­

cia indutiva e reatância capacitiva. Na maioria dos casos, porém, um ou dois destes três elementos têm tão pouca influência no circuito que podem ser desprezados.

 

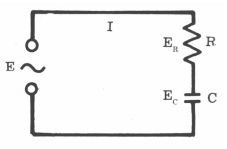
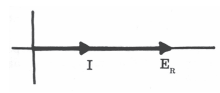
Após o estudo dos circuitos ideais veremos os circuitos monofásicos EM SÉRIE E PARALELO E MISTOS. Por sua Vez, os circuitos em série serão divididos em três grupos: circuitos R-C, circuitos R-L e circuitos R-L-C.

 

 

CIRCUITO PURAMENTE RESISTIVO

 

Trata-se de um circuito (Figura 01} em que que a única dificu1dade a ser vencida pela tensão é a resistência efetiva e portanto,

 

FIG. 01

Z=R

convém esclarecer que "R" não é apenas a resistência de um resistor e sim A RESISTENCIA EQUIVALENTE

DE TODO OS ELEMENTOS QUE CONSTITUEM O CIRCUITO.

 

A intensidade da corrente fornecida pela fonte é

 


donde

 

 

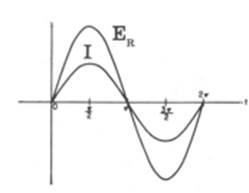
A tensão ER e a intensidade da corrente atingem valores correspondentes ao mesmo tempo:

 

FIG. 02

Quando isto ocorre com duas grandezas, dizemos que estão EM FASE. Em outras palavras, a tensão ER e a intensidade da corrente no circuito atingem seus valores máximos, mínimos ou quaisquer valores no mesmo instante. Isto é evidente, pois

 

ER = IR

R é constante.
Neste circuito temos a igualdade

 

ER = E

 

Como as duas grandezas E. e I são senoidais e estão em fase, podemos representá-las vetorialmente conforme a figura

 

FIG. 03

 

Toda a energia aplicada a este circuito é usada para vencer apenas sua resistência. Assim, podemos concluir que

 

Potência reativa = 0

Potência real = Potência aparente

 

O cálculo da potência em C.A é feito com as mesmas equações estudadas em C.C., observados apenas os seguintes fatos:

 

 

- A potência aparente refere-se à energia gasta por segundo para vencer a dificuldade total do circuito; para calculá-la devemos considerar a impedância (Z) e a tensão total aplicada ao circuito (E):

 

- Potência real é apenas a energia gasta por segundo para vencer a resistência efetiva. No seu cálculo é considerada simplesmente a resistência efetiva (R) e a tensão ER:

 


- A potência reativa é a energia gasta unicamente para vencer a reatância do circuito. Para calculá-la, consideramos a reatância (X) e a parcela da tensão destinada a vencê-la (Ex):


 

VOLTS-AMIPÊRES REATIVOS (Vars)

Como vimos, o circuito que está sendo considerado não apresenta reatância, e a potência reativa é nula.

O fator de potência do circuito é igual a I ou 100%; isto porque toda a energia aplicada ao circuito está sendo gasta para vencer sua resistência. Tam­bém pela expressão abaixo chegamos à mesma conclusão:

 

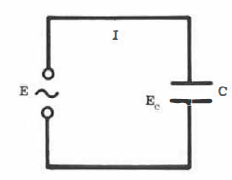
CIRCUITO PURAMENTE CAPACITIVO

 

FIG. 04

 


Neste caso, o único obstáculo ao estabelecimento de uma corrente no circuito é a reatância capacitiva. Assim, podemos escrever que

 

XC simboliza a reatância capaci­tiva total do circuito, isto é, a reatância oferecida pela capacitância equivalente do circuito.

A intensidade da corrente no circuito é

 

 

Donde

 


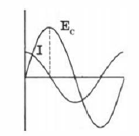
Sabemos que a d.d.p. entre as placas de um capacitor é zero quando a corrente de carga é máxima, e vice-versa. Neste circuito, E, e I não atingem valores correspondentes ao mesmo tempo

 

FIG. 05

 

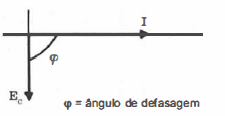
Dizemos que E, e I estão DEFASADAS de 90 graus elétricos; como os valores de I se antecipam aos valores de Ec , afirmamos que I está adiantada 90° graus elétricos em relação a Ec.

 

Como estas duas grandezas são senoidais e estão defasadas 90° graus elétricos, podemos representá-las vetorialmente de acordo com a figura


FIG. 06

 

Toda a energia aplicada a este circuito é usada para vencer sua reatância capacitiva. Concluímos que

 

Potência real = 0

Potência reativa = Potência aparente

As potências aparentes e reativa podem ser calculadas com qualquer das expressões:

 

Q=S=EI=ECI=I²Z=I²XC=E²/Z=EC²/XC

 


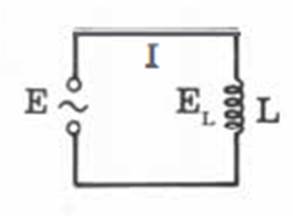
O fator de potência do circuito é zero, pois não há gasto de energia para vencer resistência, ou, como mostra a expressão a seguir:

 

 

 

CIRCUITO PURAMENTE INDUTIVO

FIG. 07

O circuito apresenta uma única dificuldade ao estabele­cimento de unia corrente elétrica: a sua reatância indutiva.

 

Desta forma podemos escrever que

Z=XL =2πfL

 

XL simboliza a reatância indutiva total do circuito; é a reatância oferecida pela autoindutância equivalente do circuito.

A intensidade da corrente no cir­cuito é

 

I = E/Z = E/XL = E/2πfL

 

 

Donde

 

E=IZ e Z=E/I

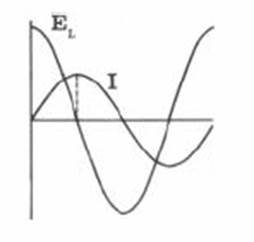
Estudamos que a indutância no circuito retarda o crescimento e a queda da corrente, e vimos que a força eletromotriz de autoindução é máxima quando I é igual a zero, e vice-versa. Portanto,


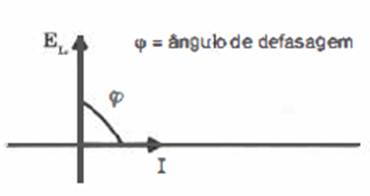
EL e I estão sempre defasados 90° graus elétricos, o que pode ser representado como mostra a figura

 

FIG. 08

 

 

Neste caso, dizemos que I está atrasada 90° graus elétricos em relação à grandeza EL.

 

Vetorialmente, podemos represen­tar estas duas grandezas do seguinte modo:

 

FIG. 09

 

A energia aplicada ao circuito tem a exclusiva finalidade de vencer a rea­tância indutiva, donde concluímos que:

 

Potência reativa = Potência aparente

 

Potência real = 0

 

As potências aparentes e reativa podem ser calculadas com qualquer das expressões abaixo:

 

Q=S=EI=ECI=I²Z=I²XL=E²/Z=EL²/ XL

 

O fator de potência do circuito é zero, porque não está sendo gasta energia para vencer resistência. Chega-se à mesma conclusão pela expressão