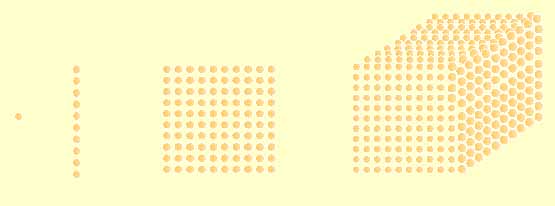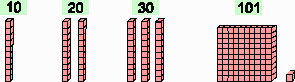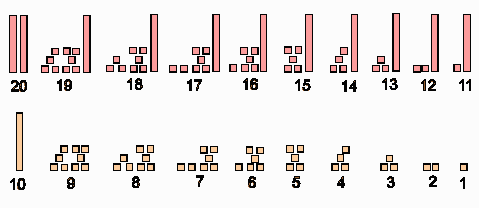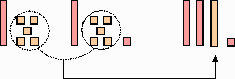MATERIAL DOURADO
Aconteceu de crianças de quatro anos de idade ficarem atraídas por esses objetos brilhantes e facilmente manejáveis. Para surpresa nossa, puseram-se a combiná-los, imitando as crianças maiores. Surgiu assim um tal entusiasmo pelo trabalho com os números, particularmente com o sistema decimal, que se pôde afirmar que os exercícios de aritmética tinham se tornado apaixonantes. As crianças foram compondo números até 1000. O desenvolvimento ulterior foi maravilhoso, a tal ponto que houve crianças de cinco anos que fizeram as quatro operações com números de milhares de unidades". O Material Dourado é um dos muitos materiais idealizados pela médica e educadora italiana Maria Montessori para o trabalho com matemática. Embora especialmente elaborado para o trabalho com aritmética, a idealização deste material seguiu os mesmos princípios montessorianos para a criação de qualquer um dos seus materiais, a educação sensorial:
Inicialmente, o Material Dourado era conhecido como "Material das Contas Douradas" e sua forma era a seguinte:
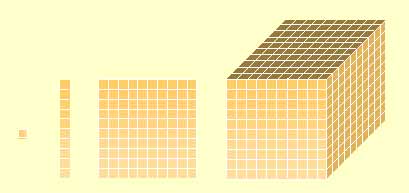
Embora esse material permitisse que as próprias crianças compusessem as dezenas e centenas, a imprecisão das medidas dos quadrados e cubos se constituía num problema ao serem realizadas atividades com números decimais e raiz quadrada, entre outras aplicações possíveis para o material de contas. Foi por isso que Lubienska de Lenval, seguidor de Montessori, fez uma modificação no material inicial e o construiu em madeira na forma que encontramos atualmente.
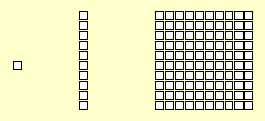
O nome "Material Dourado" vem do original "Material de Contas Douradas". Em analogia às contas, o material apresenta sulcos em forma de quadrados. Pode-se fazer uma adaptação do material dourado para o trabalho em sala de aula, com papel quadriculado de 1cm X 1 cm, onde as peças são feitas da seguinte forma:
unidade dezena centena (1 X1) (1 X 10) (10 X 10) Este material em papel possui a limitação de não ser possível a construção do bloco, o que é uma desvantagem em relação ao material em madeira. O primeiro contato do aluno com o material deve ocorrer de forma lúdica para que ele possa explorá-lo livremente. É nesse momento que a criança percebe a forma, a constituição e os tipos de peça do material. Ao desenvolver as atividades o professor pode pedir às crianças que elas mesmas atribuam nomes aos diferentes tipos de peças do material e criem uma forma própria de registrar o que vão fazendo. Seria conveniente que o professor trabalhasse durante algum tempo com a linguagem das crianças para depois adotar os nomes convencionais: cubinho, barra, placa e bloco. O material dourado destina-se a atividades que auxiliam o ensino e a aprendizagem do sistema de numeração decimal-posicional e dos métodos para efetuar as operações fundamentais (ou seja, os algoritmos). No ensino tradicional, as crianças acabam "dominando" os algoritmos a partir de treinos cansativos, mas sem conseguirem compreender o que fazem. Com o material dourado a situação é outra: as relações numéricas abstratas passam a ter uma imagem concreta, facilitando a compreensão. Obtém-se, então, além da compreensão dos algoritmos, um notável desenvolvimento do raciocínio e um aprendizado bem mais agradável. O material, mesmo sendo destinado ao trabalho com números (na matemática) pode ser utilizado com crianças de até seis anos de idade, para desenvolver a criatividade, motricidade e o raciocínio lógico-matemático.
ATIVIDADES: 1. JOGOS LIVRES Objetivo : tomar contato com o material, de maneira livre, sem regras. Durante algum tempo,
os alunos brincam com o material, fazendo construções livres. O material
dourado é construído de maneira a representar um sistema de agrupamento.
Sendo assim, muitas vezes as crianças descobrem sozinhas relações entre as
peças. Por exemplo, podemos encontrar alunos que concluem: 2. MONTAGEM Objetivo: perceber as relações que há entre as peças. O professor sugere as
seguintes montagens: O professor estimula
os alunos a obterem conclusões com perguntas como estas: Nesta atividade
também é possível explorar conceitos geométricos, propondo desafios como
estes: 3. DITADO Objetivo: relacionar cada grupo de peças ao seu valor numérico. O professor mostra, um de cada vez, cartões com números. As crianças devem mostrar as peças correspondentes, utilizando a menor quantidade delas.
Variação: 4. FAZENDO TROCAS Objetivo: compreender as características do sistema decimal. - fazer agrupamentos de 10 em 10; Para esta atividade, cada grupo deve ter um dado marcado de 4 a 9. Cada criança do grupo, na sua vez de jogar, lança o dado e retira para si a quantidade de cubinhos correspondente ao número que sair no dado. Veja bem: o número que sai no dado dá direito a retirar somente cubinhos. Toda vez que uma criança juntar 10 cubinhos, ela deve trocar os 10 cubinhos por uma barra. E aí ela tem direito de jogar novamente. Da mesma maneira, quando tiver 10 barrinhas, pode trocar as 10 barrinhas por uma placa e então jogar novamente. O jogo termina, por exemplo, quando algum aluno consegue formar duas placas. O professor então pergunta: Se houver dúvida, fazer as "destrocas". O objetivo do jogo das trocas é a compreensão dos agrupamentos de dez em dez (dez unidades formam uma dezena, dez dezenas formam uma centena, etc.), característicos do sistema decimal. A compreensão dos agrupamentos na base 10 é muito importante para o real entendimento das técnicas operatórias das operações fundamentais. O fato de a troca ser premiada com o direito de jogar novamente aumenta a atenção da criança no jogo. Ao mesmo tempo, estimula seu cálculo mental. Ela começa a calcular mentalmente quanto falta para juntar 10, ou seja, quanto falta para que ela consiga fazer uma nova troca. * cada placa será destrocada por 10 barras; * cada barra será destrocada por 10 cubinhos. Variações: Pode-se jogar com dois dados e o aluno pega tantos cubinhos quanto for a soma dos números que tirar dos dados. Pode-se utilizar também uma roleta indicando de 1 a 9. 5. PREENCHENDO TABELAS Objetivo: os mesmos das atividades 3 e 4. - preencher tabelas respeitando o
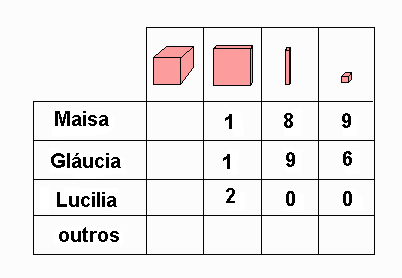
valor posicional; As regras são as mesmas da atividade 4. Na apuração, cada criança escreve em uma tabela a quantidade conseguida.
Olhando a tabela, devem responder
perguntas como estas: Olhando a tabela à procura do vencedor, a criança compara os números e percebe o valor posicional de cada algarismo. Por exemplo: na posição das dezenas, o 2 vale 20; na posição das centenas vale 200. Ao tentar determinar os demais colocados (segundo, terceiro e quarto lugares) a criança começa a ordenar os números. 6. PARTINDO DE CUBINHOS Objetivo: os mesmos da atividade 3, 4 e 5. Cada criança recebe um certo número de cubinhos para trocar por barras e depois por placas. A seguir deve escrever na tabela os números correspondentes às quantidades de placas, barras e cubinhos obtidos após as trocas. Esta atividade torna-se interessante na medida em que se aumenta o número de cubinhos.
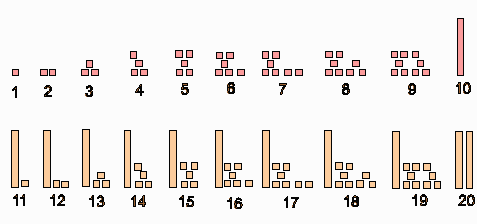
7. VAMOS FAZER UM TREM? Objetivo: compreender que o sucessor é o que tem " 1 a mais" na seqüência numérica. O professor combina com os alunos:
Quando as crianças terminarem de montar o trem, recebem papeletas nas quais devem escrever o código de cada vagão. Esta atividade leva à formação da idéia de sucessor. Fica claro para a criança o "mais um", na seqüência dos números. Ela contribui também para a melhor compreensão do valor posicional dos algarismos na escrita dos números.
8. UM TREM ESPECIAL Objetivo: compreender que o antecessor é o que tem " 1 a menos" na seqüência numérica. O professor combina com os alunos:
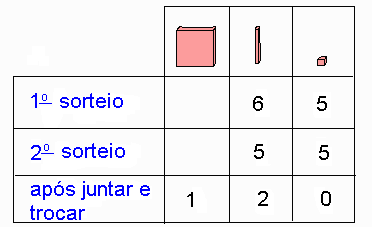
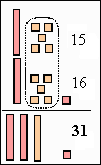
Quando as crianças terminam de montar o trem, recebem papeletas nas quais devem escrever o código de cada vagão. Esta atividade trabalha a idéia de antecessor. Fica claro para a criança o "menos um" na seqüência dos números. Ela contribui também para uma melhor compreensão do valor posicional dos algarismos na escrita dos números. 9. JOGO DOS CARTÕES Objetivos: compreender o mecanismo do "vai um" nas adições; estimular o cálculo mental. O professor coloca no centro do grupo alguns cartões virados para baixo. Nestes cartões estão escritos números entre 50 e 70. 1º sorteio: Um aluno do grupo sorteia um cartão. Os demais devem pegar as peças correspondentes ao número sorteado. Em seguida, um representante do grupo vai à lousa e registra em uma tabela os números correspondentes às quantidades de peças. 2º sorteio: Um outro aluno sorteia um segundo cartão. Os demais devem pegar as peças correspondentes a esse segundo número sorteado. Em seguida, o representante do grupo vai à tabela registrar a nova quantidade. Nesse ponto, juntam-se as duas quantidades de peças, fazem-se as trocas e novamente completa-se a tabela. Ela pode ficar assim:
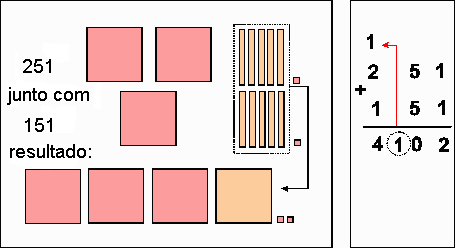
Isto encerra uma rodada e vence o grupo que tiver conseguido maior total. Depois são feitas mais algumas rodadas e o vencedor do dia é o grupo que mais rodadas venceu. Os números dos cartões podem ser outros. Por exemplo, números entre 10 e 30, na primeira série; entre 145 e 165, na segunda série. Depois que os alunos estiverem realizando as trocas e os registros com desenvoltura, o professor pode apresentar a técnica do "vai um" a partir de uma adição como, por exemplo, 15 + 16. Observe que somar 15 com 16 corresponde a juntar estes conjuntos de peças.
Fazendo as trocas necessárias,
Compare, agora, a
operação:
*com os números:
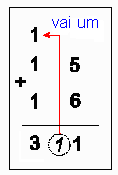
Ao aplicar o "vai um", o professor pode concretizar cada passagem do cálculo usando o material ou desenhos do material, como os que mostramos. O "vai um" também pode indicar a
troca de 10 dezenas por uma centena, ou 10 centenas por 1 milhar, etc.
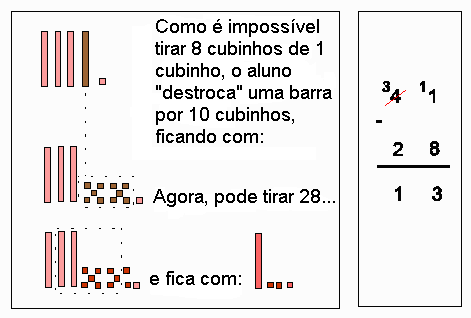
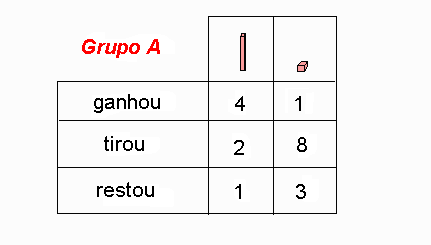
No exemplo que acabamos de ver, o "vai um" indicou a troca de 10 dezenas por uma centena. É importante que a criança perceba a relação entre sua ação com o material e os passos efetuados na operação. 10. O JOGO DE RETIRAR Objetivos: compreender o mecanismo do "empresta um" nas subtrações com recurso; estimular o cálculo mental. Esta atividade pode ser realizada como um jogo de várias rodadas. Em cada rodada, os grupos sorteiam um cartão e uma papeleta. No cartão há um número e eles devem pegar as peças correspondentes a essa quantia. Na papeleta há uma ordem que indica quanto devem tirar da quantidade que têm. Por exemplo: cartão com número 41 e papeleta com a ordem: TIRE 28.
Vence a rodada o grupo que ficar com as peças que representam o menor número. Vence o jogo o grupo que ganhar mais rodadas. É importante que, primeiro, a criança faça várias atividades do tipo: "retire um tanto", só com o material. Depois que ela dominar o processo de "destroca", pode-se propor que registre o que acontece no jogo em uma tabela na lousa. Isto irá proporcionar melhor entendimento do "empresta um" na subtração com recurso. Quando o professor apresentar essa técnica, poderá concretizar os passos do cálculo com auxílio do material ou desenhos do material. O "empresta um" também pode indicar a "destroca" de uma centena por 10 dezenas ou um milhar por 10 centenas, etc. Veja o jogo seguinte:
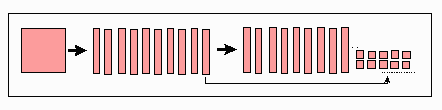
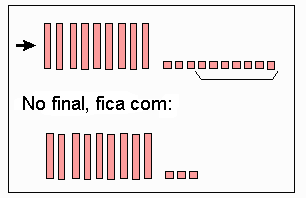
11. "DESTROCA" Objetivos: os mesmos da atividade 10. Cada grupo de alunos recebe um dado marcado de 4 a 9 e uma placa. Quando o jogador começa, todos os participantes têm à sua frente uma placa. Cada criança, na sua vez de jogar, lança o dado e faz as "destrocas" para retirar a quantidade de cubinhos correspondente ao número que sair no dado. Veja bem: esse número dá direito a retirar somente cubinhos. Na quarta rodada, vence quem ficar com as peças que representam o menor número. Exemplo: Suponha que um aluno tenha tirado 7 no dado. Primeiro ele troca uma placa por 10 barras e uma barra por 10 cubinhos:
Depois, retira 7 cubinhos:
Salientamos novamente a importância de se proporem várias atividades como essa, utilizando, de início, só o material. Quando o processo de "destroca" estiver dominado, pode-se propor que as crianças façam as subtrações envolvidas também com números.
8 – DOMINÓ Essa atividade é semelhante ao jogo de dominó. As peças serão distribuídas entre os alunos sendo que uma delas será escolhida pelo professor para ser a peça inicial do jogo. O professor estabelece o nível de dificuldade da atividade estipulando o número de diferenças que deve haver entre as peças. Supondo que deva haver uma diferença entre as peças e que a peça inicial seja um triângulo vermelho pequeno e grosso. A peça seguinte deverá conter apenas uma diferença, como por exemplo, um triângulo amarelo pequeno e grosso (a diferença nesse caso é a cor). A atividade segue até que uma das crianças termine suas peças. As demais deverão sempre conferir se a peça colocada pelo colega “serve”, ou seja, se contém o número de diferenças estipulado pela professora.
OBSERVAÇÃO: Esse material é muito utilizado no trabalho com conjuntos (notações, relação de pertinência, relação de inclusão, união e intersecção de conjuntos). As diferenças existentes entre as peças são utilizadas nessas construções e as atividades realizadas anteriormente são maneiras de internalizar estes conceitos. Após a realização dessas atividades, outras podem ser realizadas. 9 – CONJUNTO
DAS PARTES Uma criança lança o primeiro dado e retira do conjunto de blocos as peças que satisfazem a característica da face superior. Lança o segundo dado e retira do subconjunto obtido as peças que satisfazem a característica da face superior. Lança o terceiro dado e retira do último subconjunto obtido as peças que satisfazem a característica indicada no dado. Lança o quarto dado e retira a peça que satisfaz a última condição, chegando, assim, a um conjunto unitário. Variação: Se em vez de utilizarmos todas as peças da caixa escolhermos algumas peças aleatórias. Poderemos chegar à noção do conjunto vazio usando o mesmo procedimento. 10 – DESCOBRINDO A INTERSECÇÃO E A UNIÃO Entrega de dois pedaços de cordão para cada grupo para a formação de dois conjuntos. O professor solicita aos grupos que:
O professor deverá observar se os grupos atenderam corretamente as ordens dadas e solicitar aos grupos um relato do ocorrido. ***Os alunos perceberão, sem a interferência do professor, que existem peças que devem estar, simultaneamente, no interior das duas curvas. Notarão que para isto ser possível, as curvas não poderão estar separadas. Isto é, existe uma região comum entre eles onde as peças que possuem as duas características, triangulares e amarelas, ficam localizadas (O professor deve enfatizar este fato). A partir da descoberta dos alunos, o professor salientará que as curvas representam conjuntos e que a região comum entre ambas forma o conjunto intersecção. Da mesma forma, se o professor pedir para que construam um conjunto formado por todas as peças amarelas ou triangulares, teremos a definição de união de conjuntos. Variação: Usando três cordões, o professor poderá solicitar que no interior de cada curva coloquem, sucessivamente (por exemplo): - todas as peças circulares; - todas as peças azuis; - todas as peças pequenas e verificar a intersecção entre eles. ***Quando não existir a intersecção eles serão conjuntos disjuntos. 11 – A atividade número 4 seria ideal para trabalhar o conceito de pertinência. O tesouro pertence à coluna (conjunto) “Quem pegou o tesouro?” e não pertence à coluna (conjunto) “Quem não pegou o tesouro?”. Além disso, o conjunto das peças azuis e triangulares (*) está contido no conjunto das peças azuis e o conjunto das peças triangulares contém o mesmo (*).
BIBLIOGRAFIA: COSTA, Maria da Piedade Resende da. Matemática para deficientes mentais. São Paulo: EDICON, 1997. (Coleção Acadêmica. Série Comunicação) FALZETTA, Ricardo. Construa a lógica, bloco a bloco. In: Nova Escola, 111 ed., abr 1998, p.20-23. FERRARI, Márcio. A criança como protagonista. In: Nova Escola, 164 ed., ago 2003, p.32-34. PACHECO, Alice Teresinha. Material Dourado; Blocos Multibásicos. In: Educação Matemática em Revista, 4 ed., 2002, p. 51-56
|