Escoamento real
Em páginas anteriores, foi comentada a equação de Bernoulli, que vale para o escoamento de um fluido incompressível sem atrito com as paredes da tubulação.

|
| Figura 01 |
As tubulações reais, no entanto, oferecem resistência ao escoamento e isso não pode ser desprezado na maioria dos casos, sob pena de erros consideráveis.
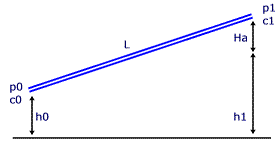
Na Figura 01 é considerada uma situação ideal. Portanto,
|
| Figura 02 |
Na Figura 02, Ha é a perda de carga.
Introduzindo esse valor na igualdade anterior,
Ou seja, para fins de cálculo, uma tubulação real é considerada uma ideal acrescida da parcela da perda de carga.
As fórmulas que permitem o cálculo da perda de carga dão em geral valores por unidade de comprimento de tubulação (perda de carga unitária), simbolizada por J. Assim,
Ha = J L #B.1#. Onde:J: perda de carga em em metro por metro (m/m)
L: comprimento da tubulação em metros (m)
O método mais preciso de cálculo da perda de carga unitária é dado pela equação de Equação de Darcy-Weisbach:
| J | perda de carga unitária | m/m |
| f | coeficiente de atrito para o escoamento | adimensional |
| c | velocidade do escoamento | m/s |
| g | aceleração da gravidade | m/s2 |
| D | diâmetro interno da tubulação | m |
A velocidade do escoamento pode ser obtida da equação da continuidade
Q = S c #C.2#, onde Q é a vazão em m3/s e S é a área da seção transversal interna do tubo em m2.A determinação do coeficiente de atrito f é mais complexa. Ele depende de dois fatores:
a) do número de Reynolds Re do escoamento, que é dado por
| c | velocidade do escoamento | m/s |
| D | diâmetro interno da tubulação | m |
| ν | viscosidade cinemática do fluido | m2/s |
Se Re < 2000 o escoamento é dito laminar. Se Re > 4000 o escoamento é dito turbulento. Entre os dois valores existe uma zona de transição, para a qual não há fórmula precisa. Na maioria dos casos práticos, os escoamentos são turbulentos.
b) do diâmetro e rugosidade das paredes da tubulação.
Com esses dados, o valor de f pode ser determinado por gráficos ou métodos iterativos. Mas o método não é objeto desta página. A alternativa mais simples é o uso de alguma fórmula empírica como a de Hazen-Williams. Alguns especialistas contemporâneos sugerem o seu abandono, alegando que os métodos computacionais estão disseminados e, portanto, não mais se justifica o uso. Mas é simples e por isso é aqui apresentada, lembrando que é uma fórmula aproximada e válida somente para instalações comuns de água.
Fórmula de Hazen-Williams
| J | perda de carga unitária | m/m |
| Q | vazão de água | m3/s |
| D | diâmetro interno da tubulação | m |
| C | coeficiente que depende do material da tubulação |
O formulário abaixo facilita o cálculo a partir de bitolas padronizadas de tubulações.
Valores adotados para o coeficiente C:
| aço galvanizado | 125 |
| aço soldado | 130 |
| cimento-amianto | 130 |
| ferro fundido revestido | 125 |
| polietileno | 120 |
| PVC ou cobre | 140 |
Perdas localizadas e comprimento equivalente
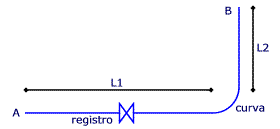
Acessórios como conexões e registros provocam perdas de carga localizadas. No cálculo, a perda localizada é representada pelo comprimento equivalente, isto é, o comprimento de tubulação da mesma bitola que produz a mesma perda de carga.
|
| Figura 01 |
Ltotal = L1 + L2 + Lequiv_registro + Lequiv_curvaE a perda de carga total é dada conforme igualdade já vista:
Ha = J Ltotal
A próxima página contém tabelas de comprimentos equivalentes para alguns tipos de acessórios comuns de tubulações.