BLOCOS LÓGICOS

A Geometria exige uma maneira específica de raciocinar, explorar e descobrir, fatores que desempenham importante papel na concepção de espaço pela criança.
As figuras geométricas mais conhecidas pelos alunos são o quadrado, o retângulo, o triângulo e o círculo que são trabalhadas desde a Educação Infantil até o Ensino Médio.
Nas classes de educação infantil, os blocos lógicos, pequenas peças geométricas, criadas na década de 50 pelo matemático húngaro Zoltan Paul Dienes, são bastante eficientes para que os alunos exercitem a lógica e evoluam no raciocínio abstrato. Foram utilizados de modo sistemático com crianças pelo psicólogo russo Vygotsky (1890-1934), quando ele estudava a formação dos conceitos infantis.

Eles facilitarão a vida dos alunos nos futuros encontros com números, operações, equações e outros conceitos da disciplina.
Sua função é dar aos alunos idéias das primeiras operações lógicas, como correspondência e classificação. Essa importância atribuída aos materiais concretos tem raiz nas pesquisas do psicólogo suíço Jean Piaget (1896-1980).
Segundo Piaget, a aprendizagem da Matemática envolve o conhecimento físico e o lógico-matemático. No caso dos blocos, o conhecimento físico ocorre quando o aluno manuseia, observa e identifica os atributos de cada peça.
O lógico-matemático se dá quando ela usa esses atributos sem ter o material em mãos (raciocínio abstrato).

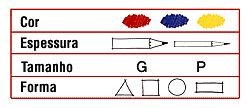
Material : um jogo de blocos lógicos contém 48 peças divididas em três cores (amarelo, azul e vermelho), quatro formas (círculo, quadrado, triângulo e retângulo), dois tamanhos (grande e pequeno) e duas espessuras (fino e grosso).

Alunos: a turma estará dividida em pequenos grupos para a realização das atividades.

1 - JOGO LIVRE
Primeiramente, os alunos reconhecerão o material. Formarão desenhos com as formas dos blocos lógicos, observando e comparando as cores, os tamanhos e as formas. Esse trabalho poderá ser feito em grupo, pois os alunos, através de diálogos, enriquecerão o conhecimento das características físicas de cada bloco.

Trenzinho feito com círculos, quadrados e retângulos:
formas livres no primeiro contato das crianças
com as peças dos blocos lógicos.

2 - EMPILHANDO PEÇAS
Peças do material espalhadas pela mesa (ou pelo chão). Cada aluno deverá pegar uma peça e colocar no centro do grupo, de modo que as peças serão empilhadas uma a uma. O aluno deverá fazer de tudo para a “torre” não cair. Para isso os alunos terão que pensar nas peças mais adequadas para a base, meio ou topo da torre deixando as “piores” para o companheiro seguinte. Nesta atividade os alunos desenvolverão a capacidade de discernimento, raciocínio lógico e motricidade.

3 - JOGO DA CLASSIFICAÇÃO
Apresentar um quadro às crianças para que classifiquem os blocos.
Criar junto com os alunos os atributos que serão dados para os tipos de blocos existentes.
Exemplos:
a) as quatro formas: círculo, quadrado, retângulo e triângulo
b) as duas espessuras: grosso e fino
c) os dois tamanhos: pequeno e grande
d) as cores: amarelo, azul e vermelho
Fazer em cartolina um quadro. Escolher alguns atributos e pedir aos alunos que separem os blocos de acordo com os atributos escolhidos.
Primeiramente, escolher apenas um atributo (quadrada).
Exemplo: separar apenas as peças quadradas.
Depois, ir acrescentando atributos (vermelha, fina, pequena).
Os alunos irão completar o quadro com a peça quadrada, pequena, fina e vermelha.

4 - A HISTÓRIA DO PIRATA
Agora, contar a seguinte história: "Era uma vez um pirata que adorava tesouros. Havia no porão de seu navio um baú carregado de pedras preciosas. Nesse porão, ninguém entrava. Somente o pirata tinha a chave. Mas sua felicidade durou pouco. Numa das viagens, uma tempestade virou seu barco e obrigou todos os marinheiros a se refugiarem numa ilha. Furioso, o pirata ordenou que eles voltassem a nado para resgatar o tesouro. Mas, quando retornaram, os marujos disseram que o baú havia sumido. 'Um de vocês pegou', esbravejou o pirata desconfiado."

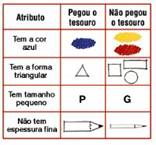
Nesse ponto, começa o jogo com as crianças. Peça que cada uma escolha um bloco lógico. Ao observar as peças sorteadas, escolha uma delas sem comunicar às crianças qual é. Ela será a chave para descobrir o "marujo" que está com o tesouro. Apresente então um quadro com três colunas (veja abaixo). Supondo que a peça escolhida seja um triângulo pequeno, azul e grosso, você diz: "Quem pegou o tesouro tem a peça azul". Pedindo a ajuda das crianças, preencha os atributos no quadro. Em seguida, dê outra dica: "Quem pegou o tesouro tem a forma triangular". Siga até chegar ao marinheiro que esconde o tesouro. A atividade estimula mais que a comparação visual. Também exercita a comparação entre o atributo, agora imaginado pela criança, e a peça que a criança tem na mão. A negação (segunda coluna do quadro) leva à classificação e ajuda a compreender, por exemplo, que um número pertence a um e não a outro conjunto numérico.

5 – JOGO ADIVINHE QUAL É A PEÇA
Dividir a classe em grupos e espalhar os blocos lógicos pelo chão. Para descobrir qual é a peça, as crianças farão uma competição. Dar um comando das características de uma peça (por exemplo: amarelo, triângulo, grande e fino) para um grupo.
Em seguida, o grupo deve procurar e selecionar a peça correspondente para mostrá-la, o mais rapidamente possível, às outras equipes.
A competição poderá ter como objetivo verificar qual grupo encontra a peça correta primeiro ou de qual grupo encontra mais peças corretas. À medida que acertam, recebem uma pontuação.
Outra opção é de cada equipe desafiar os outros grupos da classe distribuindo eles mesmos os atributos.

6- O JOGO DAS DIFERENÇAS
Neste jogo os alunos observarão três peças sobre o quadro.
Exemplo:
1- triângulo, amarelo, grosso e grande;
2- quadrado, amarelo, grosso e grande;
3- retângulo, amarelo, grosso e grande;
Eles deverão escolher a quarta peça (círculo, amarelo, grosso e grande) observando que, entre ela e sua vizinha, deverá haver o mesmo número de diferenças existente entre as outras duas peças do quadro (a diferença na forma).
As peças serão colocadas pela professora de forma que, em primeiro lugar, haja apenas uma diferença. Depois duas, três e, por fim, quatro diferenças entre as peças. Os alunos farão comparações cada vez mais rápidas quando estiverem pensando na peça que se encaixe em todas as condições.
 

7 - SIGA OS COMANDOS

As crianças vão transformar uma peça em outra seguindo uma seqüência de comandos estabelecida pelo professor. Esses comandos são indicados numa linha por setas combinadas com atributos. No exemplo da foto, vemos uma seqüência iniciada com os atributos círculo, azul e grosso. As crianças então escolhem a peça correspondente. O comando seguinte é mudar para a cor vermelha. As crianças selecionam um círculo grosso e vermelho. Em seguida, devem mudar para a espessura fina. Então, um círculo vermelho e fino é selecionado. Assim por diante, o professor pode continuar acrescentando comandos ou pode apresentar uma seqüência pronta. Depois é feito o processo inverso.

As crianças são então apresentadas a uma nova seqüência de comandos, já com a última peça. Elas deverão reverter os comandos para chegar à peça de partida. A atividade é essencial para o entendimento das operações aritméticas, principalmente a soma como inverso da subtração e a multiplicação como inverso da divisão. E também contribui, no futuro, para que as crianças resolvam problemas e entendam demonstrações, atividades que exigem uma forma de raciocínio em etapas seqüenciais.

8 – DOMINÓ

Essa atividade é semelhante ao jogo de dominó. As peças serão distribuídas entre os alunos sendo que uma delas será escolhida pelo professor para ser a peça inicial do jogo. O professor estabelece o nível de dificuldade da atividade estipulando o número de diferenças que deve haver entre as peças. Supondo que deva haver uma diferença entre as peças e que a peça inicial seja um triângulo vermelho pequeno e grosso. A peça seguinte deverá conter apenas uma diferença, como por exemplo, um triângulo amarelo pequeno e grosso (a diferença nesse caso é a cor). A atividade segue até que uma das crianças termine suas peças. As demais deverão sempre conferir se a peça colocada pelo colega “serve”, ou seja, se contém o número de diferenças estipulado pela professora.

OBSERVAÇÃO:

Esse material é muito utilizado no trabalho com conjuntos (notações, relação de pertinência, relação de inclusão, união e intersecção de conjuntos). As diferenças existentes entre as peças são utilizadas nessas construções e as atividades realizadas anteriormente são maneiras de internalizar estes conceitos.

Após a realização dessas atividades, outras podem ser realizadas.

9 – CONJUNTO DAS PARTES
Para essa atividade são necessários quatro dados: um com o desenho dos blocos em cada face (triângulo, quadrado, círculo e retângulo), outro com as faces coloridas (azul, amarelo e vermelho), outro com a grandeza (grande e pequeno) e outro com a espessura (grosso e fino).

Uma criança lança o primeiro dado e retira do conjunto de blocos as peças que satisfazem a característica da face superior. Lança o segundo dado e retira do subconjunto obtido as peças que satisfazem a característica da face superior. Lança o terceiro dado e retira do último subconjunto obtido as peças que satisfazem a característica indicada no dado. Lança o quarto dado e retira a peça que satisfaz a última condição, chegando, assim, a um conjunto unitário.

Variação:

Se em vez de utilizarmos todas as peças da caixa escolhermos algumas peças aleatórias. Poderemos chegar à noção do conjunto vazio usando o mesmo procedimento.

10 – DESCOBRINDO A INTERSECÇÃO E A UNIÃO

Entrega de dois pedaços de cordão para cada grupo para a formação de dois conjuntos. O professor solicita aos grupos que:

• retiram da caixa todas as peças triangulares e todas as todas as peças amarelas.
• coloquem no interior de uma das curvas todas as peças amarelas e, a seguir, na outra, todas as triangulares.

O professor deverá observar se os grupos atenderam corretamente as ordens dadas e solicitar aos grupos um relato do ocorrido.

***Os alunos perceberão, sem a interferência do professor, que existem peças que devem estar, simultaneamente, no interior das duas curvas. Notarão que para isto ser possível, as curvas não poderão estar separadas. Isto é, existe uma região comum entre eles onde as peças que possuem as duas características, triangulares e amarelas, ficam localizadas (0 professor deve enfatizar este fato).

A partir da descoberta dos alunos, o professor salientará que as curvas representam conjuntos e que a região comum entre ambas forma o conjunto intersecção.

Da mesma forma, se o professor pedir para que construam um conjunto formado por todas as peças amarelas ou triangulares, teremos a definição de união de conjuntos.

Variação:

Usando três cordões, o professor poderá solicitar que no interior de cada curva coloquem, sucessivamente (por exemplo):

- todas as peças circulares;

- todas as peças azuis;

- todas as peças pequenas

e verificar a intersecção entre eles.

***Quando não existir a intersecção eles serão conjuntos disjuntos.

11 – A atividade número 4 seria ideal para trabalhar o conceito de pertinência. O tesouro pertence à coluna (conjunto) “Quem pegou o tesouro?” e não pertence à coluna (conjunto) “Quem não pegou o tesouro?”. Além disso, o conjunto das peças azuis e triangulares (*) está contido no conjunto das peças azuis e o conjunto das peças triangulares contém o mesmo (*).

BIBLIOGRAFIA:

COSTA, Maria da Piedade Resende da. Matemática para deficientes mentais. São Paulo: EDICON, 1997. (Coleção Acadêmica. Série Comunicação)

FALZETTA, Ricardo. Construa a lógica, bloco a bloco. In: Nova Escola, 111 ed., abr 1998, p.20-23.

FERRARI, Márcio. A criança como protagonista. In: Nova Escola, 164 ed., ago 2003, p.32-34.

PACHECO, Alice Teresinha. Material Dourado; Blocos Multibásicos. In: Educação Matemática em Revista, 4 ed., 2002, p. 51-56