Grandezas Vetoriais

As grandezas vetoriais representam tudo aquilo que pode ser medido (mensurável) e necessita de uma direção e sentido. As grandezas vetoriais se diferenciam das grandezas escalares por necessitares de sentido.

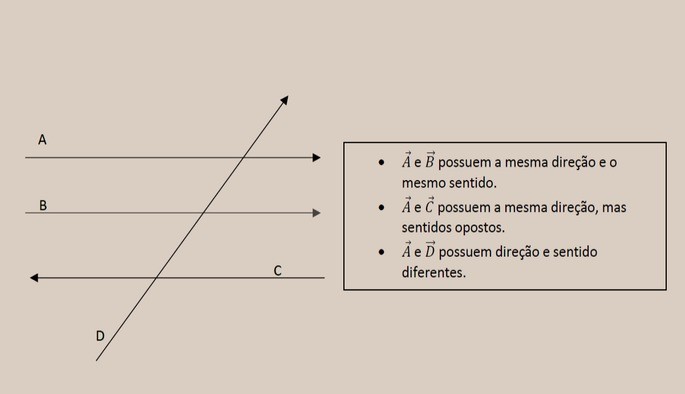
Essa relação com o modo, o sentido e a direção são chamados de vetor. Na matemática, o vetor é uma reta que possui uma direção. Por exemplo, do ponto A para o ponto B e é representada por vet(AB).

Grandezas vetoriais e grandezas escalares

As grandezas escalares assumem um sentido completo a partir de sua medida (módulo). É o que ocorre com grandezas como: tempo, temperatura, massa e volume.

Outras grandezas físicas necessitam, além do módulo, de um sentido e uma direção para serem compreendidas. Essas são chamadas de grandezas vetoriais.

O vetor é uma reta orientada que possui uma direção, um sentido e um módulo. É a forma de representar as grandezas vetoriais.

Os vetores variam de acordo com seu sentido e direção

Exemplos de grandezas vetoriais

São alguns exemplos de grandezas físicas que necessitam de sentido e direção:

Grandeza Vetorial	Definição	Unidade de Medida
Velocidade	Distância percorrida por um corpo em um espaço de tempo.	m/s; cm/s, km/h…
Aceleração	Taxa de variação de velocidade.	cm/s^2(Gal); m/s^2…
Força	Ente responsável pelo movimento ou deformação de um corpo.	N, kgf, dina, lbf…
Campo Elétrico	Campo de força provocado pela ação de forças elétricas.	N/C, V/m…
Campo Magnético	Campo de ação do magnetismo criado por uma carga magnética.	A/m, Oe

Interessou? Veja também:

· Vetores: soma, subtração e decomposição