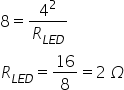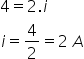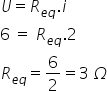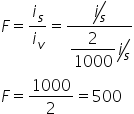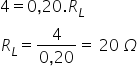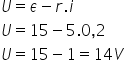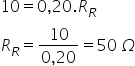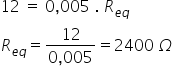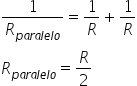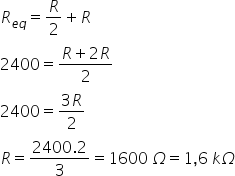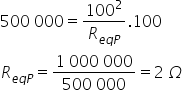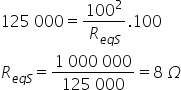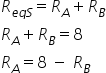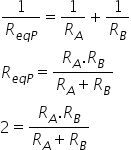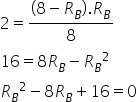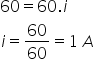Associação de Resistores - Exercícios

Resistores são elementos de um circuito elétrico que transformam energia elétrica em calor. Quando dois ou mais resistores aparecem em um circuito podem estar associados em série, paralelo ou misto.

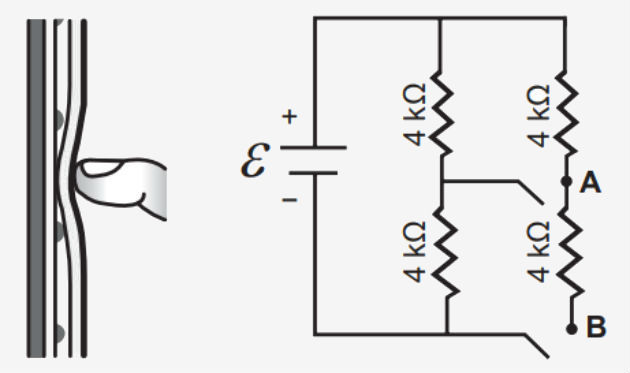
Questões sobre associação de resistores caem com frequência nos vestibulares e fazer exercícios é uma ótima maneira de verificar seu conhecimento sobre esse importante assunto da eletricidade.

Questões Resolvidas e Comentadas

1) Enem - 2018

Muitos smartphones e tablets não precisam mais de teclas, uma vez que todos os comandos podem ser dados ao se pressionar a própria tela. Inicialmente essa tecnologia foi proporcionada por meio das telas resistivas, formadas basicamente por duas camadas de material condutor transparente que não se encostam até que alguém as pressione, modificando a resistência total do circuito de acordo com o ponto onde ocorre o toque. A imagem é uma simplificação do circuito formado pelas placas, em que A e B representam pontos onde o circuito pode ser fechado por meio do toque.

Qual é a resistência equivalente no circuito provocada por um toque que fecha o circuito no ponto A?

a) 1,3 kΩ
b) 4,0 kΩ
c) 6,0 kΩ
d) 6,7 kΩ
e) 12,0 kΩ

Resposta

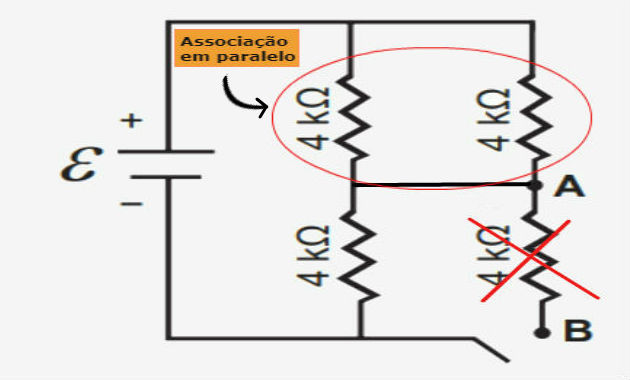
Como apenas a chave A foi conectada, então a resistência ligada aos terminais AB não funcionará.

Desta forma, temos três resistências, duas ligadas em paralelo e em série com a terceira, conforme mostrado na imagem abaixo:

Para começar, vamos calcular a resistência equivalente da ligação em paralelo, para isso, partiremos da seguinte fórmula:

A resistência equivalente da associação em paralelo está associada em série com a terceira resistência. Sendo assim, podemos calcular a resistência equivalente desta associação fazendo:

R_eq = R_paralelo + R3

Substituindo os valores das resistência, temos:

R_eq = 2 + 4 = 6 kΩ

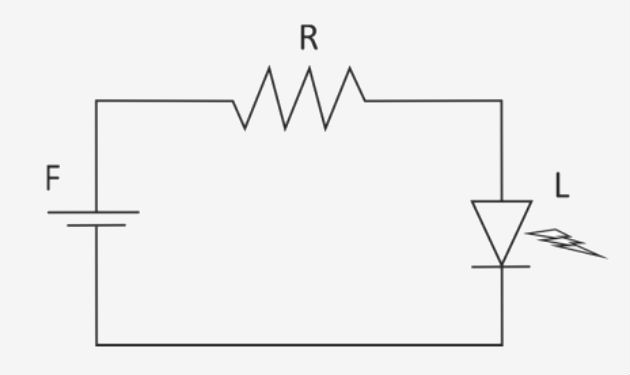
Alternativa: c) 6,0 kΩ

2) Fuvest - 2018

Atualmente são usados LEDs (Light Emitting Diode) na iluminação doméstica. LEDs são dispositivos semicondutores que conduzem a corrente elétrica apenas em um sentido. Na figura, há um circuito de alimentação de um LED (L) de 8 W, que opera com 4 V, sendo alimentado por uma fonte (F) de 6 V.

O valor da resistência do resistor (R), em Ω , necessário para que o LED opere com seus valores nominais é, aproximadamente,

a) 1,0.
b) 2,0.
c) 3,0.
d) 4,0.
e) 5,0.

Resposta

Podemos calcular o valor da resistência do LED através da fórmula da potência, ou seja:

Substituindo os valores indicados na questão, temos:

A corrente que atravessa o circuito pode ser encontrada aplicando a 1ª lei de Ohm, ou seja:

U = R . i

Então, calculando a corrente que atravessa o LED, encontramos:

Como o LED e o resistor estão associados em série, a corrente que atravessa o LED é a mesma em todo o circuito.

Com isso, podemos encontrar a resistência equivalente do circuito, considerando o valor da tensão da fonte e da corrente do circuito, ou seja:

Para encontrar o valor da resistência, basta aplicar a fórmula da resistência equivalente de um circuito em série, isto é:

R_eq = R + R_LED

Substituindo os valores, temos:

3 = R + 2
R = 3 - 2 = 1 Ω

Alternativa: a) 1,0.

3) Unicamp - 2018

Nos últimos anos, materiais exóticos conhecidos como isolantes topológicos se tornaram objeto de intensa investigação científica em todo o mundo. De forma simplificada, esses materiais se caracterizam por serem isolantes elétricos no seu interior, mas condutores na sua superfície. 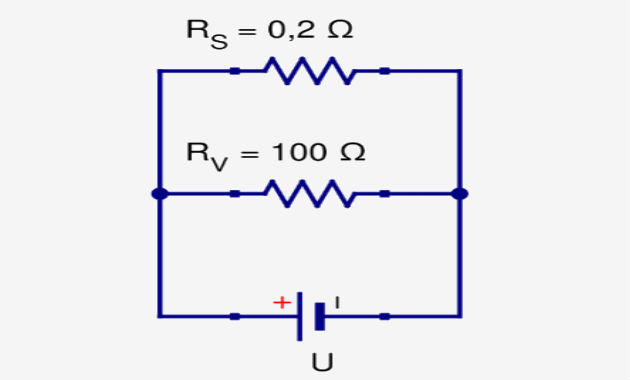Desta forma, se um isolante topológico for submetido a uma diferença de potencial U , teremos uma resistência efetiva na superfície diferente da resistência do seu volume, como mostra o circuito equivalente da figura abaixo. Nessa situação, a razão  entre a corrente i_s que atravessa a porção condutora na superfície e a corrente i_v que atravessa a porção isolante no interior do material vale

a) 0,002
b) 0,2
c) 100,2
d) 500

Resposta

Os resistores R_v e R_s estão associados em paralelo. Neste tipo de associação, todos os resistores ficam submetidos a mesma diferença de potencial U.

Entretanto, a intensidade da corrente que atravessa cada resistor será diferente, pois os valores das resistências são diferentes. Assim, pela 1ª lei de Ohm temos:

U = R_s.i_s e U = R_v.i_v

Igualando as equações, encontramos:

Isolando i_v e substituindo os valores das resistências, temos:

Para encontrar o valor da razão F, vamos substituir i_v pela expressão encontrada, ou seja:

Alternativa: d) 500.

4) UFRGS - 2018

Uma fonte de tensão cuja força eletromotriz é de 15 V tem resistência interna de 5 Ω. A fonte está ligada em série com uma lâmpada incandescente e com um resistor. Medidas são realizadas e constata-se que a corrente elétrica que atravessa o resistor é de 0,20 A, e que a diferença de potencial na lâmpada é de 4 V. Nessa circunstância, as resistências elétricas da lâmpada e do resistor valem, respectivamente,

a) 0,8 Ω e 50 Ω
b) 20 Ω e 50 Ω
c) 0,8 Ω e 55 Ω
d) 20 Ω e 55 Ω
e) 20 Ω e 70 Ω

Resposta

Na associação em série, a corrente que atravessa o circuito é a mesma, logo, a corrente de 0,20 A também atravessa a lâmpada. Então, aplicando a lei de Ohm, temos:

Podemos calcular o valor da diferença de potencial entre os terminais do circuito através da equação do gerador, ou seja:

A diferença de potencial entre os terminais da lâmpada é igual a 4 V e a d.d.p. de todo o circuito é igual a 14 V. Então, nos terminais do resistor a diferença de potencial é igual a 10 V (14-4).

Agora que conhecemos o valor da d.d.p. no resistor, podemos aplicar a lei de Ohm:

Alternativa: b) 20 Ω e 50 Ω.

5) PUC/RJ - 2018

Um circuito tem 3 resistores idênticos, dois deles colocados em paralelo entre si, e ligados em série com o terceiro resistor e com uma fonte de 12 V. A corrente que passa pela fonte é de 5,0 mA. Qual é a resistência de cada resistor, em kΩ?

a) 0,60
b) 0,80
c) 1,2
d) 1,6
e) 2,4

Resposta

Como conhecemos o valor da tensão nos terminais do circuito e a corrente que o atravessa, podemos calcular o valor da resistência equivalente aplicando a lei de Ohm, ou seja:

U = R . i

Substituindo os valores e considerando que 5,0 mA é igual a 0,005 A, temos:

A resistência equivalente do circuito é igual a soma da resistência equivalente da associação em paralelo com a terceira resistência em série.

Sendo assim precisamos encontrar o valor da resistência equivalente do paralelo, para isso, iremos aplicar a seguinte fórmula:

Desta forma, podemos calcular o valor de cada resistência a partir do valor da resistência equivalente do circuito, ou seja:

Alternativa: d) 1,6

6) PUC/SP - 2018

Dois resistores elétricos, de resistências R_A e R_B, geram 500 kWh de energia, quando associados em paralelo e submetidos a uma tensão elétrica de 100 V, durante 100 horas ininterruptas. Esses mesmos resistores, quando associados em série e submetidos à mesma tensão, durante o mesmo intervalo de tempo, geram 125 kWh de energia.

Determine, em ohm, os valores de R_A e R_B, respectivamente:

a) 4 e 8.
b) 2 e 8.
c) 2 e 4.
d) 4 e 4.

Resposta

A energia elétrica é dada pela fórmula E = P.t, onde P é a potência elétrica e t é o tempo. A potência, por sua vez, pode ser encontrada através da expressão . Portanto, podemos escrever a energia como:

Desta forma, vamos substituir os valores para cada associação. Na associação em paralelo, temos:

Na associação em série, a resistência equivalente será igual a:

Agora que conhecemos o valor das resistências equivalentes em cada uma das associações, podemos calcular o valor das resistências R_A e R_B aplicando a fórmula de resistores equivalentes.

Na série:

No paralelo:

Substituindo R_A nesta expressão, temos:

Resolvendo essa equação do 2º grau, encontramos que R_B = 4 Ω. Substituindo esse valor para encontrar o valor de R_A:

R_A = 8 - R_B
R_A = 8 - 4 = 4 Ω

Alternativa: d) 4 e 4.

7) Enem - 2017

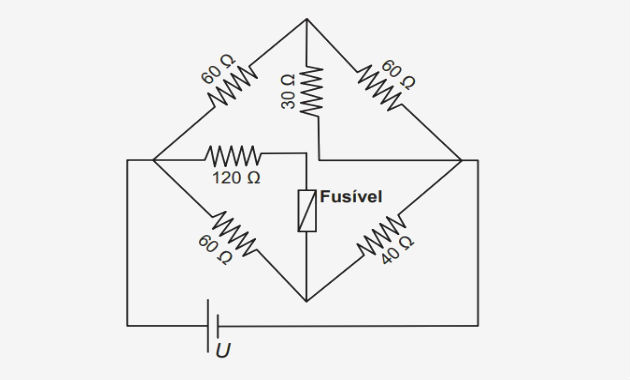
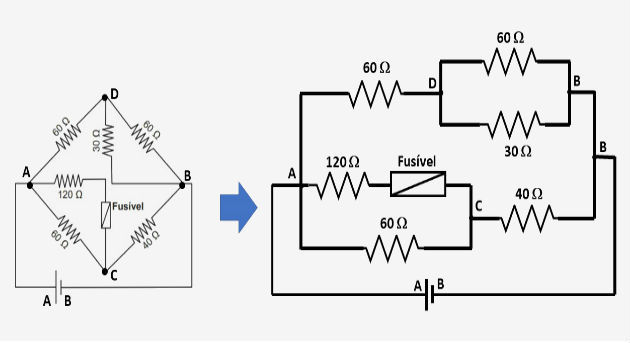
Fusível é um dispositivo de proteção contra sobrecorrente em circuitos. Quando a corrente que passa por esse componente elétrico é maior que sua máxima corrente nominal, o fusível queima. Dessa forma, evita que a corrente elevada danifique os aparelhos do circuito. Suponha que o circuito elétrico mostrado seja alimentado por uma fonte de tensão U e que o fusível suporte uma corrente nominal de 500 mA.

Qual é o máximo valor da tensão U para que o fusível não queime?

a) 20 V
b) 40 V
c) 60 V
d) 120 V
e) 185 V

Resposta

Para melhor visualizar o circuito, vamos redesenhá-lo. Para isso, nomeamos cada nó do circuito. Assim, podemos identificar que tipo de associação existe entre os resistores.

Observando o circuito, identificamos que entre os pontos A e B temos dois ramos em paralelo. Nestes pontos, a diferença de potencial é a mesma e igual a diferença de potencial total do circuito.

Desta forma, podemos calcular a diferença de potencial em apenas um ramo do circuito. Sendo assim, vamos escolher o ramo que contém o fusível, pois neste caso, conhecemos a corrente que o atravessa.

Note que a corrente máxima que poderá percorrer o fusível é igual a 500 mA (0,5 A) e que essa corrente também irá percorrer o resistor de 120 Ω.

A partir dessa informação, podemos aplicar a lei de Ohm para calcular a diferença de potencial neste trecho do circuito, ou seja:

U_AC = 120.0,5 = 60 V

Esse valor corresponde a d.d.p. entre os pontos A e C, portanto, o resistor de 60 Ω também está submetido a esta tensão, pois está associado em paralelo ao resistor de 120 Ω.

Conhecendo a d.d.p. que o resistor de 120 Ω está submetido, podemos calcular a corrente que o atravessa. Para isso, vamos novamente aplicar a lei de Ohm.

Então, a corrente que atravessa o resistor de 40 Ω é igual a soma da corrente que atravessa o resistor de 120Ω com a que atravessa o resistor de 60 Ω, ou seja:

i´= 1 + 0,5 = 1,5 A

Com essa informação, podemos calcular a d.d.p. entre os terminais do resistor de 40 Ω. Assim, temos:

U_CB = 1,5.40 = 60 V

Para calcular a tensão máxima para que o fusível não queime, será necessário apenas calcular a soma de U_AC com U_CB, portanto:

U = 60 + 60 = 120 V

Alternativa: d) 120 V