A-
CARGA ELÉTRICA
|
1- É dado um corpo eletrizado com carga 6,4 mC. Determine
o número de elétrons em falta no corpo. A carga do elétron é -1,6. 10-19 C. |
||||||||||||||||
|
2- De um corpo neutro retiramos 104 elétrons.
Ele ficou com carga elétrica negativa ou positiva? Qual é o valor de sua carga elétrica? |
||||||||||||||||
|
3- Quantos elétrons em excesso têm o corpo eletrizado com
carga –16nC. |
||||||||||||||||
|
4- De um corpo neutro retiramos 104 elétrons.
Ele ficou com carga elétrica negativa ou positiva? Qual é o valor de sua carga elétrica? |
||||||||||||||||
|
5- Um corpo foi eletrizado com uma carga de +32 μC.
Determine sua polaridade e quantos elétrons foram retirados ou doados. |
||||||||||||||||
|
6- De uma determinada esfera foram retirados 2x1012
elétrons. Determine o valor da carga elétrica adquirida pela esfera e seu sinal. |
||||||||||||||||
|
7- Ao se atritar um bastão de ebonite com um pano de lã,
observa-se que o ebonite perde cerca de 4x108 elétrons para a lã. Determine: Expresse
a resposta em mC (miliCoulomb). a) a polaridade e o valor da carga elétrica adquirida
pelo bastão de ebonite. b) a polaridade e o valor da carga elétrica adquirida
pelo pano de lã. |
||||||||||||||||
|
8- Uma partícula está eletrizada positivamente com uma
carga elétrica de 4.10–15 C. Como o módulo da carga do elétron é 1,6.10–19
C, essa partícula: a) ganhou 2,5. 104 elétrons b) perdeu 2,5. 104 elétrons c) perdeu 6,4. 104 elétrons d) ganhou 6,4. 104 elétrons |
||||||||||||||||
|
9- Têm-se três esferas metálicas A, B e C eletrizadas.
Aproximando-se uma da outra constata-se que A atrai B e B repele C. Então podemos afirmar que: a) A e B possuem cargas positivas e C possui carga
negativa. b) A e B possuem cargas negativas e C possui carga
positiva. c) A e C possuem carga de mesmo sinal e B possui carga
de sinal contrário ao sinal de A. d) A e C possuem cargas de sinais contrários e B possui
carga de sinal contrário ao sinal de A. |
||||||||||||||||
|
10- Dispõe-se de quatro esferas metálicas: P, Q, R e S.
Sabe-se que P repele Q, que P atrai R, que R repele S e que S está carregada positivamente. Pode-se
dizer que: a) Q tem carga negativa. b) P e R têm cargas de mesmo sinal. c) P e Q estão carregadas positivamente. d) P está carregada positivamente. |
||||||||||||||||
|
11- Um aluno tem 4 esferas idênticas, pequenas e condutoras
(A, B, C e D), carregadas com cargas respectivamente iguais a 5Q, 3Q, 6Q e 1Q. A esfera A é
colocada em contato com a esfera B e a seguir com as esferas C e D. Ao final do processo a esfera A
estará carregada com a carga equivalente a: a) 7,5Q b) 6Q c) 3Q d) 1Q |
||||||||||||||||
|
12- Charles Augustin de Coulomb (1736-1806), físico
francês, iniciou suas pesquisas no campo da eletricidade e do magnetismo para participar de um
concurso aberto pela Academia de Ciências sobre a fabricação de agulhas imantadas. Estudou o atrito e
descobriu a eletrização superficial dos condutores. Em sua homenagem a unidade de carga elétrica
no sistema internacional recebeu seu nome. Qual o número de elétrons existentes em uma carga
de 1 C? (Considere e = 1,6.10– 19 C). a) 1,6.10 –19 elétrons. b) 1 elétron. c) 1,6.1019 elétrons. d) 6,25.1018 elétrons. |
||||||||||||||||
|
13- Um corpo tem 2.1018 elétrons e 4.1018
prótons. Como a carga elétrica de um elétron (ou de um próton) vale, em módulo, e=1,6.10-19 C (carga
elementar) pode-se afirma que o corpo está carregado com uma carga elétrica de: a) 0,32 C b) –0,32 C c) 0,64 C d) – 0,64 C |
||||||||||||||||
|
14- Réptil de Alta Adesão! Como a lagartixa consegue subir
na parede? A aderência entre as patas Das lagartixas e a superfície das paredes é resultado do
mesmo fenômeno atrativo eletromagnético que garante a estabilidade dos átomos e moléculas, a chamada
força de Van der Waals. As pontas dos dedos desses répteis possuem cerca de 2 milhões de pelos
finíssimos, chamados setas, e a extremidade de cada pelo subdivide-se em até mil
filamentos de dimensões microscópicas conhecidos como cerdas. Os extremos de cada cerda são carregados
eletricamente. Os milhões de cerdas fazem com que as lagartixas troquem elétrons entre suas patas
e a superfície da parede ou do teto. Este processo é conhecido como força de Van der Waals. Esse
fenômeno só foi confirmado em 2000 com a publicação, na revista científica britânica Nature, de
um estudo coordenado pelos biólogos Kellar Autumn e Robert Full e pelos engenheiros Ronald Fearing
e Thomas Kenny, todos americanos. Revista Galilei, fevereiro de 2002, Nº 127, pg 21. Sabendo-se que a lagartixa tem 20 dedos, cada dedo tem
2.000.000 de setas e cada seta 1.000 cerdas e que cada cerda tenha perdido 5.000 elétrons
então, a carga elétrica total do dedos vale: Dado: e = 1,6x10-19 C a) 5x10-6 C b) 12x10-9 C c) 3,2x10-5 C d) 6x10-6 C |
||||||||||||||||
|
15- De acordo com o modelo atômico atual, os prótons e
nêutrons não são mais considerados partículas elementares. Eles seriam formados de três
partículas ainda menores, os quarks. Admite-se a existência de 12 quarks na natureza, mas só dois tipos
formam os prótons e nêutrons, o quark up (u), de carga elétrica positiva, igual a 2/3 do valor da
carga do elétron, e o quark down (d), de carga elétrica negativa, igual a 1/3 do valor da carga do elétron.
A partir dessas informações, assinale a alternativa que apresenta corretamente a composição do
próton e do nêutron:
|
||||||||||||||||
|
16- Pessoas que têm cabelos secos observam que, em dias
secos, quanto mais tentam assentar seus cabelos, penteando-os, mais eles ficam eriçados. Isso
pode ser explicado do seguinte modo: a) Os cabelos ficam eletrizados por atrito. b) Os cabelos ficam eletrizados por indução
eletrostática. c) Os cabelos ficam eletrizados por contato. d) Os cabelos adquirem magnetismo. e) Trata-se sim de um fenômeno puramente biológico. |
B- CORRENTE ELÉTRICA
|
17- Calcule a intensidade da corrente elétrica em um
condutor que a cada 2 segundos passam por ele uma quantidade de carga elétrica igual a 5 C. |
||||
|
18- Calcule o tempo necessário para que uma corrente de 2 A
forneça uma quantidade de carga elétrica igual a 150 C. |
||||
|
19- Uma lâmpada é percorrida por uma corrente de 0,5 A
durante um intervalo de 30 segundos. Calcule a quantidade de carga elétrica
que atravessou a lâmpada neste intervalo. |
||||
|
20- Numa secção reta de um condutor de eletricidade, passam
12 C de carga elétrica a cada minuto. Calcule a intensidade da corrente
elétrica, em ampères, neste condutor. |
||||
|
21- Numa secção transversal de um fio condutor passa uma
carga de 10 C a cada 2,0s. Calcule a intensidade da corrente elétrica neste
fio. |
||||
|
22- Pela secção reta de um fio, passam 5,0.1018
elétrons a cada 2,0 s. Sabendo-se que a carga elétrica elementar vale 1,6.10-19C,
calcule a corrente elétrica que percorre o fio. |
||||
|
23- Pelo filamento de uma lâmpada passam 2.1016 elétrons
em um intervalo de tempo de 5 ms. Sabendo-se que a carga elétrica elementar vale 1,6.10-19
C, calcule a intensidade da corrente elétrica nesta lâmpada. |
||||
|
24- Uma corrente elétrica de intensidade 16 A percorre um
condutor metálico. A carga elétrica elementar é e = 1,6.10-19 C. Calcule o número
de elétrons que atravessam uma secção transversal desse condutor em 1,0 min. |
||||
|
25- Uma lâmpada permanece acesa durante 5 minutos, por
efeito de uma corrente de 2 A. Nesse intervalo de tempo, calcule a carga total (em C)
fornecida a essa lâmpada. |
||||
|
26- Uma corrente elétrica de intensidade 11,2 μA
percorre um condutor metálico. A carga elementar é e = 1,6.10-19 C. Determine o tipo e o número
de partículas carregadas que atravessam uma seção transversal desse condutor por segundo. |
||||
|
27- Um condutor é percorrido por uma corrente de 50 mA
durante um intervalo de tempo de 2minutos. Calcule o número de elétrons que
atravessam uma secção transversal desse condutor. |
||||
|
28- Calcule o tempo que uma carga de 4 μC gasta para
atravessar uma secção transversal de um condutor percorrido por uma corrente de 5 mA. |
||||
|
29- Um carregador de celular tem como especificações de
saída a seguinte inscrição: 5V/500mA, onde 5 V correspondem a tensão de saída
e 500 mA a máxima corrente que ele pode fornecer. Supondo que ao conectá-lo
em um celular a corrente seja sempre constante é igual ao valor máximo,
determine qual a quantidade de carga elétrica absorvida pelo celular
conectado durante uma hora ao carregador. |
||||
|
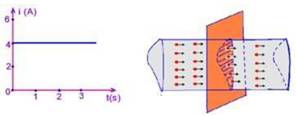
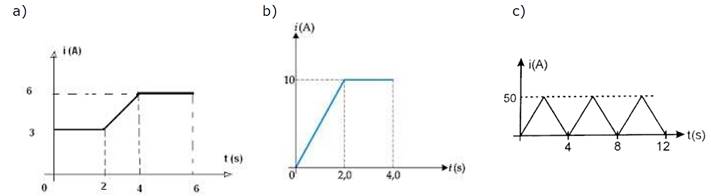
30- O gráfico da figura representa a intensidade da corrente
elétrica i em um fio condutor, em função do tempo transcorrido t. Calcule a
carga elétrica Q que passa por uma seção do condutor nos dois primeiros segundos. |
|
|||
|
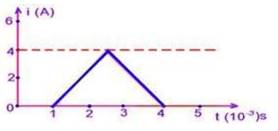
31- Um circuito eletrônico foi submetido a um pulso de
corrente indicada no gráfico. Calcule a carga elétrica que fluiu no circuito
durante esse pulso, em Coulombs. |
|
|||
|
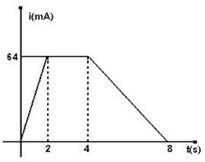
32- O gráfico mostra, em função do tempo t, o valor da
corrente elétrica i através de um condutor. Sendo Q a carga elétrica que
circulou no intervalo de tempo de 0 a 4,0, calcule a carga elétrica que
circulou no intervalo de tempo de 4,0s a 8,0s. |
|
|||
|
33- Se uma bateria de automóvel possui aproximadamente 54
A.h de capacidade de carga, qual a capacidade de carga (q) em Coulomb (C) e o número de
elétrons (n) que ela pode fornecer? |
||||
|
34- Uma bateria de caminhão tem uma capacidade de carga de
200 A.h. Determine: a) durante quanto tempo ela poderá fornecer uma corrente
de 10 A. b) durante quanto tempo ela poderá fornecer uma corrente
de 20 A. c) durante quanto tempo ela poderá fornecer uma corrente
de 50 A. d) qual a relação entre a corrente e o tempo para esta
bateria? |
||||
|
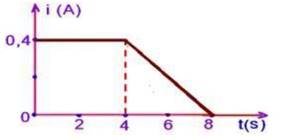
35- O gráfico ao lado mostra a variação da corrente em função do tempo em uma lâmpada. Determine a quantidade
de carga que atravessou o filamento desta lâmpada nos seguintes intervalos: a) 0 s a 2 s. b) 2 s a 4 s. c) 4 s a 8 s. d) 0 s a 8 s. |
|
|||
|
36- Calcule a corrente média para os seguintes gráficos:
|
||||
C- 1ª LEI DE OHM
|
37- Um resistor de 12 Ω é percorrido por uma
corrente de 2 A. Calcule a tensão elétrica em seus terminais. |
||||
|
38- Calcule a corrente em um resistor de 18 Ω
quando submetido a uma tensão de 12 V. |
||||
|
39- Um certo resistor é conectado aos terminais de
uma bateria de 24 V. Determine sua resistência sabendo-se que a corrente que passa pelo mesmo é
de 3 A. |
||||
|
40- Qual a resistência de um ferro de solda que
solicita uma corrente de 0,8333 A a 120 V? |
||||
|
41- Uma torradeira com resistência de 8,27 Ω
opera com uma corrente de 13,9 A. Encontre a tensão aplicada? |
||||
|
42- Qual a resistência interna de uma secadora de
roupas 127 V, que solicita uma corrente de 23,3 A? |
||||
|
43- Num resistor de 2,0 Ω, a intensidade da
corrente elétrica é 2,0 A. Qual é a tensão aplicada? |
||||
|
44- Um resistor está sob tensão de 9V, e nele passa
uma corrente de 2,25 A. Determine qual é a resistência deste resistor. |
||||
|
45- Um eletricista desejando calcular a resistência
elétrica do resistor de um chuveiro, mediu a tensão da rede elétrica e a corrente no mesmo encontrando
os seguintes respectivos valores: 125 V e 52 A. Com base nestes valores, calcule a resistência do
chuveiro. |
||||
|
46- Um resistor de 2,2 KΩ de resistência
elétrica é percorrido por uma corrente de 5 mA. Calcule a tensão em seus terminais. |
||||
|
47- Qual a corrente que percorre um resistor de 15
kΩ, quando submetido a uma d.d.p. de 12 V. |
||||
|
48- Uma corrente de 30 μA percorre um resistor
cuja d.d.p. em seus terminais vale 127 V. Calcule o valor deste resistor em kΩ. |
||||
|
49- Uma tensão de 50 mV é aplicada em um resistor de
2,7 kΩ. Calcule a corrente no mesmo. |
||||
|
50- Um resistor ôhmico, quando submetido a uma ddp de
40 V, é atravessado por uma corrente elétrica de intensidade 20 A. Quando a corrente
que o atravessa for igual a 4 A, qual será a
ddp, em volts? |
||||
|
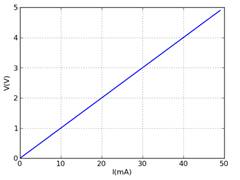
51- Dado o gráfico da tensão em função da corrente
para um resistor de resistência R, determine: a) o valor da resistência R em Ohms. b) a tensão no resistor quando for atravessado por
uma corrente de 25 mA. |
|
|||
|
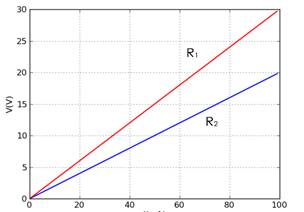
52- O gráfico ao lado mostra a relação tensão corrente
para dois resistores. Determine: a) a resistência de cada um deles. b) como podemos graficamente determinar qual dos
dois possui a maior resistência elétrica? |
|
|||
|
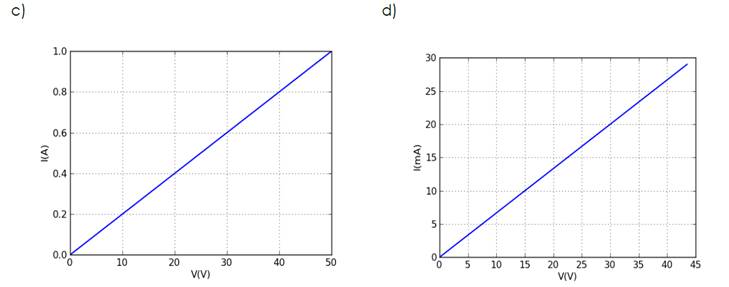
53- Para os seguintes gráficos tensão versus
corrente, determine o valor da resistência elétrica dos respectivos resistores. |
||||
|
|
||||
D- 2ª LEI DE OHM
|
54- Sabendo que a resistência de um chuveiro elétrico é
feita de um fio enrolado de níquel, calcule o comprimento do fio do resistor desse chuveiro, cuja
resistência vale 7,8Ω. Dados: Área da seção transversal do fio = 1 mm2, Resistividade do
níquel = 7,8x10-8 Ω.m. |
|
55- O filamento de tungstênio de uma lâmpada tem resistência
de 20Ω a 20oC. Sabendo-se que sua secção transversal
mede 1,1x10-4 mm2 e que a resistividade do tungstênio a
20oC é 5,5x10-2Ω.mm2.m-1,
determine o comprimento do filamento. |
|
56- Calcule a área da secção transversal que deve possuir um
fio de alumínio com resistividade 2,8x10-8Ω.m e comprimento
de 12 m, que possua uma resistência elétrica de 33,6 mΩ. |
|
57- Cada um dos 20 geradores da Usina Hidrelétrica de Ilha
Solteira fornece corrente alternada com uma diferença de potencial de,
aproximadamente, 13,8 kV em seus terminais. Essa tensão é elevada para 440 kV
e enviada para os centros consumidores através de linhas de longa distância
conhecidas como linhas de transmissão. Uma dessas linhas de transmissão liga
Ilha Solteira à subestação de Embu-Guaçu, na Grande São Paulo, numa extensão
de 680 km, usando cabos de alumínio com área de secção reta de 3,2 x 10-4
m2. Qual a resistência elétrica de cada um desses fios? A
resistividade elétrica do alumínio é de 2,8 x 10-8 Ω.m. |
|
58- Você constrói três resistências elétricas, RA, RB e RC,
com fios de mesmo comprimento e com as seguintes características: I. O fio de RA tem resistividade 1,0·10–6
Ω·m e diâmetro de 0,50 mm. II. O fio de RB tem resistividade 1,2·10–6
Ω·m e diâmetro de 0,50 mm. III. O fio de RC tem resistividade 1,5·10–6
Ω·m e diâmetro de 0,40 mm. Pode-se afirmar que: a) RA > RB > RC. b) RB > RA > RC. c) RB > RC > RA. d) RC > RA > RB. e) RC > RB > RA. |
|
59- Levando em consideração que a segunda lei de Ohm seja
dada por: a) Que o fio metálico possua uma grande área de secção
transversal. b) Que o fio metálico possua uma grande área de secção
transversal e pequeno comprimento. c) Que o fio metálico possua uma pequena área de secção
transversal e grande comprimento. d) Que o fio metálico possua pequena resistividade. e) Que o fio metálico possua uma pequena área de secção
transversal e pequeno comprimento. |
|
60- Dois fios, um de cobre com resistividade 1,7 x 10-8
Ω.m e outro de alumínio com resistividade 2,8 x 10-8Ω.m,
possuem mesmo comprimento e mesmo diâmetro. Se ambos forem percorridos pela
mesma corrente i, pode-se afirmar que: a) As resistências ôhmicas dos dois fios são iguais. b) A ddp é menor no fio de cobre. c) O fio de cobre fica submetido a um campo elétrico
maior do que o do fio de alumínio. d) A perda de energia pelo efeito Joule é menor no fio de
alumínio. |
|
61- Um fio de cobre com resistividade 1,69 x 10- 8
Ω.m é enrolado em um suporte cilíndrico, com raio 10 cm, com 500 voltas.
Sendo o raio do fio 2 mm, sua resistência elétrica, em ohms, é: |
|
62- Um fio condutor homogêneo de secção transversal
constante de área A e comprimento L, tem resistência elétrica R. Este fio é
dividido em 10 pedaços iguais que são ligados em paralelo, formando um cabo,
cuja resistência vale RC. Determine a relação entre RC e R. |
|
63- Considerem-se dois fios condutores de mesmo material: o
primeiro com diâmetro 0,6 mm, comprimento 6m e resistência de 12 Ω e o
segundo com diâmetro 0,4 mm, comprimento 4 m e resistência X Ω. Calcule
o valor da resistência do segundo condutor. |
|
64- Um condutor de secção transversal constante e
comprimento L tem resistência elétrica R. Cortando-se o fio pela metade, sua
resistência elétrica será igual a: a) 2R b) R/2 c) R/4 d) 4/R e) R/3 |
|
65- Um fio de cobre tem um raio igual a r, uma resistência R
e comprimento L. Se o raio do fio for duplicado e o comprimento reduzido à
metade, o novo valor da resistência vale: a) 4R b)
R/4 c) R d) R/8 e) 8R |
|
66- Um condutor cilíndrico de comprimento L tem resistência
elétrica R. Sendo estirado até um comprimento 2L, mantendo o mesmo volume, a
resistência elétrica será igual a: a) 4R b)
2R c) R d) R/2 e) R/4 |
|
67- Uma companhia distribuidora de eletricidade utiliza em
seus postes de transmissão dois tipos de cabos. Os dois modelos de cabos são
constituídos por fios cilíndricos de alumínio com resistividade igual a
2,8.10-8 Ω.m. Um modelo é constituído por um maço de 7 fios
de alumínio enquanto que o outro é constituído por um maço de 19 fios.
Considerando-se que os fios têm comprimentos iguais, calcule a relação entre
as resistências elétricas do cabo mais fino em comparação ao cabo mais
grosso. |
|
68- Um resistor
submetido a uma d.d.p. de 5 V é percorrido por uma corrente de 2 A. Calcule a
potência dissipada por ele. |
|
69- Ao ser
ligado a uma tomada de 127 V, um ferro de passar roupas é percorrido por uma
corrente de 8 A. Determine: a) sua resistência elétrica; b) a potência dissipada por ele. |
|
70- Um chuveiro
elétrico possui os seguintes valores nominais: 220V/5400W. Determine: a)
sua resistência elétrica b) sua
corrente nominal |
|
OBSERVAÇÕES: |